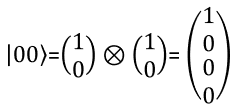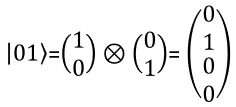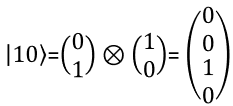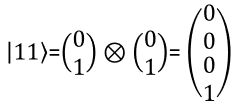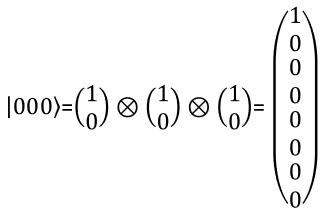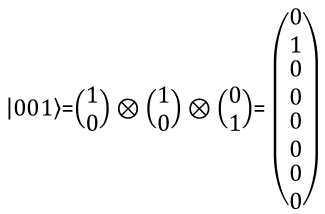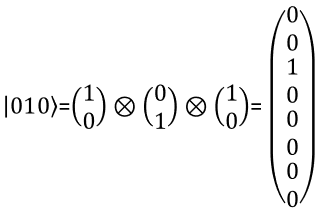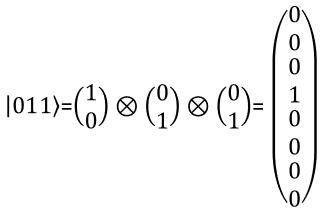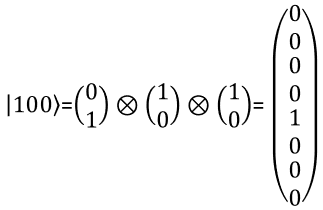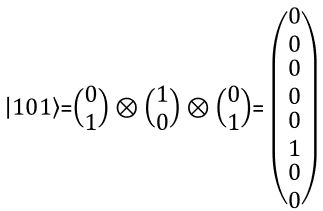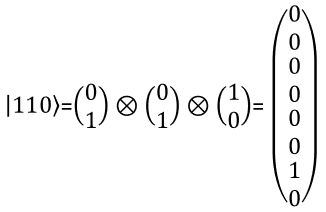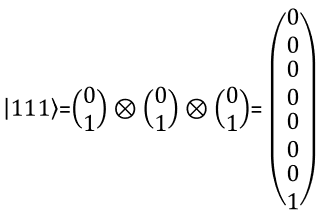|
Quantum Computing |
||
|
Qbit/Qubit
What is Qbit ? It stands for Quantum bit, but I am not going to explain on what is Qbit in this page. For this kind of explanation, I think some of the video in the video link page would do better job. Do not expect to understand the concept just by watching one or two videos. Try to find as many different ones as possible and watch all of them rather than watching only one video so over and over.
For now, just take that Qbit is the basic processing unit in Quamtum computing as the basic processing unit in ordinary computing (classical computing) is called a bit.
The critical differece between Qbit and ordinary Bit is that Qbit acts according to fundamental nature of quantum mechanics called Superposition and Entanglement (don't ask me what these are -:).
Again there are a lot of videos trying to explain on these concept).
As mentioned before, it would be very difficult to explain on the definition of Qbit(Qubit) verbally. Even if it is possible, I don't think I can capable of explaining it better than what others do in many blog and youTube. What I am trying to do here is just to give you a few keywords that you can begin with or simply using it as a keyword when you do googling. Qbit is the basic unit in Quantum Computing and it has following basic nature of quamtum mechanics and this is the main difference between Qbit and Bit (The classical bit : the unit that we use in our regular computing).
Everybody would now know how a bit is represented in ordinary computing. It is represented by two numbers 0 and 1. But is this 0 and 1 a real physical entity ? Now you also know the 0 and 1 is not the physical entity. When they are talking about physical entities for the bit 0 or 1, some people try to explain it with some physical electric switch On and Off. or if they want to go a little bit deeper into technology they may talk about some kind of transistor with the operation voltage of 5V or 3.3V or 1.8V etc. However they are trying to explain on the physical entities to the logical bits 0 and 1, it would be almost impossible to get yourself fully understood about it unless you are a physist working specifically on this area. There are still so many physists and engineers working only in the area of implemeting the physical entities for the logical bit 0 and 1. But almost everybody working with computer programming for hobby or for job can do their job just based on the concept of logical bit 0 or 1 without much or almost no knowledge on the physical entities of the logical bit. The reason why I am talking about this is for those people who claim that I cannot learn any new technologies without completely understanding the fundamental knowledge on how it works. I used to a person of this kind and still try to all my best to understand a new technology as much in fundamentals as possible. So I was reluctant to trying Quamtum computing (Quantum Programming) without mastering Quatum Theory/Quantum Mechanics. As time goes on, I started realizing that it is as if I say "I say I would not try to learn C programing or Python programming unless I master the study of solid state physics on transister". What I am trying to say is... what I am trying to explain (tyring to learn at the same time) in my note is mostly about logical entities of a Quamtum bit which can be understood without the deep knowledge of physics theory behind it. The only remaining hurdle is that you still need to get familiar with a little bit of math at this stage. I believe that the time will come in the future when even this kind of simple math would not be required in quantum computing, but for now (Dec 2019) I don't think we can avoid some simple math since quantum computing is at such an early stage like early stages of ordinary computing programming in machine code or assembly code.
Now let's get down to the job talking about Qbit. As we make an analogy between logical bits and physical entities (like transistor voltage), they have invented a logical concept in quantum mechnics which is called a spin. There are two types of spin. One is called Upspin representing spining in counter clockwise and the other one is called downspin representing spinining in clockwise. Is there any physical entities like an electron or an atom spinning around ? Physist say No. They say 'spin' is a kind of logical concept representing the nature of a quamtum particle and they can be explained only in mathematical model. It does not really mean that we can see an electron or an atom spinning in front of our eyes. So for now, let's just accept that a quamtum bit is represented by two different spin called upspin and downspin.
Just accepting all of the logical concept as given to us, let's look further into how a quamtum bit is represented. I illustrated various way of representing a quantum bit as shown below.
The left most one is how upspin is represented graphically. The next strange symbol | >. This symbol is called Bra-ket. |0> represents the quatom bit 0. And then you see a vector. This vector also represent the quatum bit 0. The last one also reprents the quatum bit 0 in a probability function and in a coordinate system. I will talk a little bit detail about this later.
The left most one is how downspin is represented graphically. |1> represents the quatom bit 1. And then you see a vector. This vector also represent the quatum bit 1. The last one also reprents the quatum bit 1 in a probability function and in a coordinate system. I will talk a little bit detail about this later.
The horizontal axis of the coordinate system indicates the probability of the bit existing as a quatum bit 0 and the vertical axis indicate the probability of the bit existing as a quamtum bit 1 as indicated below.
Very important thing to note here is 'alpha and beta are complex numbers'.
This probability function (Quamtum State function) is represented in a vector notation as follows. You should be very familiar with this notation because this will be the basis for all the operators in quantum programming. Make practice as much as possible on translating a state vector in plain language.
The number of this vector (defined as below) should be 1 as below.
If alpha and beta is complex numbers, the total probability is calculated as follows (i.e, multiplying each value with its complex conjugate).
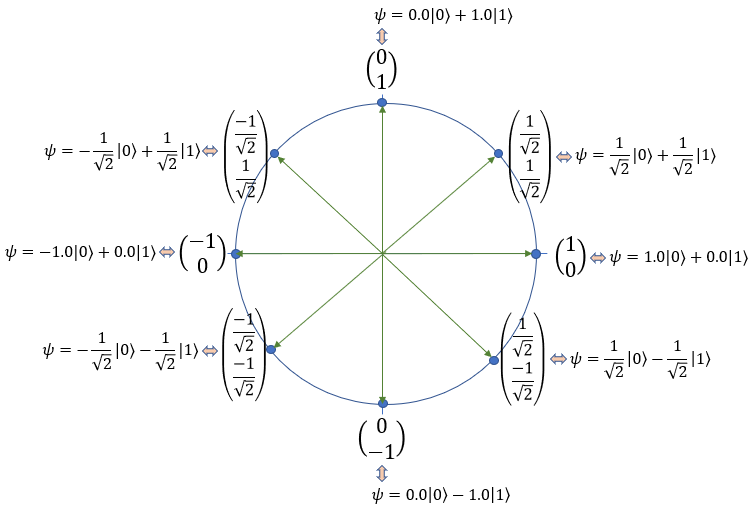
Since the norm of the state vector is 1, all the possible states represted by the state vector should all be on the peripheral of a unit circle. Some of the most commonly used state vector is mapped onto a unit circle as below. Try to translate each location marked here in plain language. For example, [1/Sqr(2) 1/Sqr(2)] indicates that the bit would be existing as the quantum bit 0 with the probability of 50% and be existing as the quantum bit 1 with the probability of 50%.
What is the meaning of Phase of Q state ?
I think I can understand (at least I got familiar to) the meaning of amplitude of the coefficient (alpha and beta) in quantum state function as described above. But it is not that clear to me about the practical meaning of the phase of the complex coefficient. I want to talk a bit about it. I just have some chat with chatGPT and I think it explains better than I do :). So I am just copying and paste from the chat here. If I get more clear understandings of my own and can explain better, I will revise this part or add my personal description.
The "phase" in this context refers to a complex number that describes the relationship between two quantum states. In particular, the phase is related to the probability of measuring a particular outcome in a quantum measurement. To understand this, let's start with the basics of quantum mechanics. In quantum mechanics, a quantum state is represented by a wave function, which is a mathematical object that describes the probability of measuring different outcomes when we make a measurement on the system. The wave function is a complex-valued function, which means that it has both a magnitude and a phase. The magnitude of the wave function tells us the probability of measuring a particular outcome. For example, if we are measuring the position of a particle, the magnitude of the wave function at a particular point tells us the probability of finding the particle at that point. The phase of the wave function, on the other hand, does not directly affect the probability of measuring a particular outcome. Instead, it affects the way that the wave function interferes with other wave functions. This interference is what gives rise to many of the strange and counterintuitive properties of quantum mechanics, such as superposition and entanglement. To make this more concrete, let's consider a simple example. Suppose we have a quantum state that is represented by a wave function with a phase of e^(iθ), where θ is some angle. If we make a measurement of this state, we will get a result with some probability that depends on the magnitude of the wave function. However, if we have another state with a wave function that also has a phase of e^(iθ), these two states can interfere with each other in a way that depends on their relative phase. Specifically, if the phases are aligned (i.e., θ is the same for both states), they will interfere constructively, and we will see an enhancement in the probability of measuring certain outcomes. If the phases are misaligned, they will interfere destructively, and we will see a suppression in the probability of measuring certain outcomes.
NOTE : Yet, it is not clear exactly what it mean by the term 'interaction' / 'interference' in this context and asked chatGPT further. Following is what chatGPT explains
Interference of electrons: One classic experiment in quantum mechanics involves firing electrons through a double-slit apparatus, which consists of two parallel slits that are separated by a small distance. When electrons are fired through the slits one at a time, they produce a pattern of bright and dark fringes on a detector screen behind the slits, indicating the probability of detecting an electron at various locations. This pattern of fringes arises from the interference of the electron waves as they pass through the slits and interfere with each other on the other side. In particular, the pattern of fringes depends on the phase relationship between the electron waves as they pass through the two slits.
If the phases are aligned, the waves will interfere constructively and produce bright fringes where the peaks of the waves add up
If the phases are misaligned, the waves will interfere destructively and produce dark fringes where the peaks of one wave cancel out the troughs of another.
The phase difference between the two waves depends on the path length difference between the two slits, and can be calculated using the wave properties of the electrons.
Entangled qubits: Another example of the role of phase in quantum mechanics involves entangled qubits, which are quantum bits that are correlated in a way that cannot be explained by classical physics. Suppose we have two qubits, labeled A and B, that are in an entangled state such that their wave function is:
|ψ> = (1/sqrt(2)) (|0_A> |1_B> - |1_A> |0_B>)
Here, |0_A> and |1_A> represent the two possible states of qubit A, and similarly for qubit B. The factor of 1/sqrt(2) ensures that the wave function is normalized, i.e., the sum of the probabilities of all possible outcomes adds up to 1.
The phase of this wave function is -1, which means that the two qubits are in a superposition of being both in the state |0> and both in the state |1>, but with a relative phase of π between these two possibilities. This phase relationship is crucial for the entanglement between the two qubits, because it ensures that the probabilities of measuring the two qubits in the same state or in different states are perfectly correlated.
In other words, if we measure qubit A and find it in the state |0>, we know with certainty that qubit B will be in the state |1>, and vice versa. This is true regardless of how far apart the two qubits are, and it is a consequence of the phase relationship between the two possibilities in the superposition.
These are just a couple of examples to illustrate the role of phase in quantum mechanics. The phase can affect many other aspects of quantum systems, including the behavior of photons, atoms, and molecules, and it is a fundamental concept in the study of quantum mechanics.
I hope you got familiar with how to represent single Qbit in mathematical format especially in a vector notation. Then would there be any way to represent two bits in a vector ? There should be. But how ? Is there any generic way to represent the multiple Qbit into a vector ? Yes, there is. The way to represent the multiple qbit into a vector is to multiply multiple single qbit vector with kronecker operator as shown below. For those who is not familiar with kronecker multiplication, refer to my math tutorial on kronecker multiplication / tensor multiplication.
The meaning of each numbers in the state vector is interpreted as follows.
This vector can be represented in the form of a probability function as shown below.
Since each of the coefficient indicate the probability for the specific bit combination, following equation should be met.
With the same logic as you present two qbit in a vector, you can represent a three qbit in a vector as shown below. You can extend the same logic to represent N qbits.
How the result of a quantum operation is measured ?
This is also from chatGPT (GPT 4.0) for my question : how the result of a quantum computing is measured ? should it repeat the same computation many times and get the probability of each quantum states ?
Following is the answer from chatGPT. Measuring the result of a quantum computation involves a process called "quantum measurement" or "projective measurement." When you measure a quantum system, it collapses from a superposition of multiple states to a single definite state, with a probability determined by the square of the amplitude associated with that state. This collapse is inherently probabilistic, and the quantum system doesn't always yield the same result in each measurement.
To obtain a reliable result from a quantum computation, you typically follow these steps: i) Run the quantum algorithm: First, execute the quantum algorithm on a quantum computer by applying a sequence of quantum gates to an initial state of qubits. This process manipulates the quantum states to perform the computation. ii) Measure the output state: After the algorithm is complete, measure the qubits' final state. The quantum computer will return a classical bit string, which corresponds to one of the possible outcomes of the computation. The probability of obtaining a specific outcome depends on the quantum state's amplitudes. iii) Repeat the process: Since the measurement process is probabilistic, you need to repeat steps i) and ii) multiple times to build a statistical distribution of the outcomes. By performing the computation and measurement many times, you can estimate the probabilities associated with each possible outcome. iv) Analyze the results: Once you have a distribution of outcomes, you can analyze the results to extract the most likely or desired outcome, depending on the problem you are solving. In some cases, post-processing techniques or classical algorithms can be used to refine the results further.
Following question : Is there any rule of thumb regarding how many times should be repeated to get reliable result ?
There isn't a one-size-fits-all rule of thumb for the number of repetitions needed to obtain reliable results in quantum computing because the required repetitions depend on the specific algorithm, problem, and desired level of confidence or accuracy. However, there are some general guidelines to consider when determining the number of repetitions:
Follow up question : If we need to repeat the measurement to get the reliable result ? shouldn't it be inefficient comparing to classical computing which requires only one run ?
It's true that quantum computing often requires multiple repetitions of a computation to obtain reliable results due to the probabilistic nature of quantum measurements. However, this does not necessarily make quantum computing inefficient compared to classical computing. There are several reasons why quantum computing can still be more efficient than classical computing for specific problems:
Follow up question : Is the 'Select number of shots' in IBM Q circuit Run option indicates the number of the repeation of circuit execution and the measurement for final outcome ?
Yes, the "Select number of shots" option in IBM Quantum Experience's circuit Run option indicates the number of times the circuit will be executed and measured to obtain the final outcome. By selecting a specific number of shots, you are instructing the quantum computer or simulator to repeat the experiment that many times, and then collect the measurement results for each execution.
The measurement outcomes from each shot are stored and used to create a histogram or a counts dictionary, which shows the number of times each classical bit string (corresponding to a particular outcome) was observed. This information allows you to estimate the probabilities of each outcome.
Selecting a higher number of shots typically leads to more accurate results because it helps build a better statistical distribution of the outcomes. However, increasing the number of shots also increases the total execution time, so you'll need to balance the desired accuracy with the available computational resources and time.
|
||