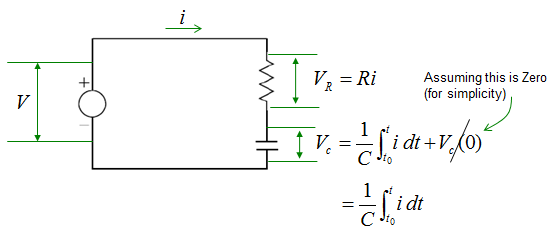|
Engineering Math - Differential Equation |
||
|
Electric Circuit
This pages will give you some examples modeling the most fundamental electrical component and a few very basic circuits made of those component. The component and circuit itself is what you are already familiar with from the physics class in high school. So I don't explain much about the theory for the circuits in this page and I don't think you need much additional information about the differential equation either. I am just gathering all of these examples in this single page just for a kind of cheatsheet for you and for myself.
Followings are the components and circuits that will be modeled in this page.
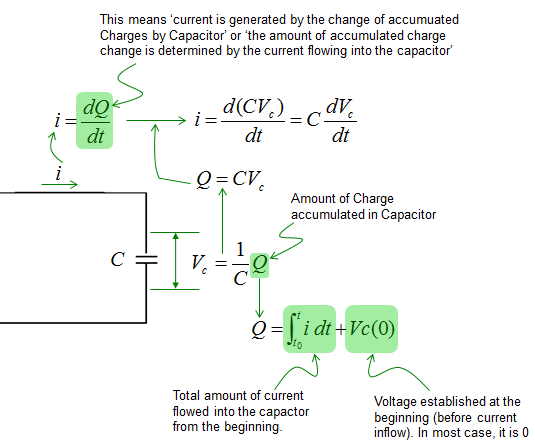
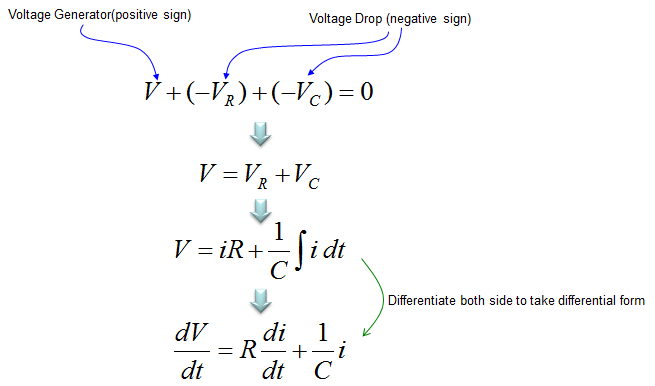
The voltage across a capacitor is described as shown below. Since most of the governing equation for electrical component is described in terms of Voltage, I would describe the circuit so as to calculate the voltage across the component. But in some cases you would need to describe the circuit so as to calculate the current or charges. In that case you would need to modify the equation to give you the right form of equation.
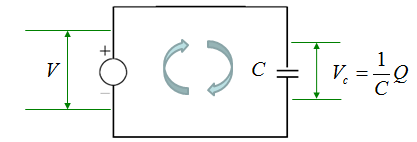
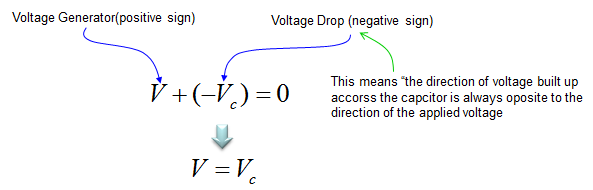
Now let's assume that we have a very simple circuit with a Voltage source and a capacitor. It can be described as below.
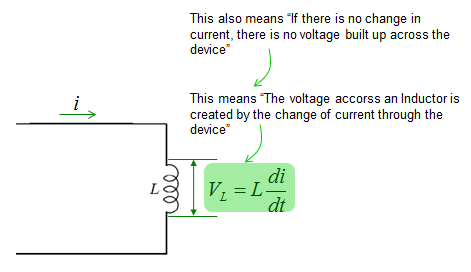
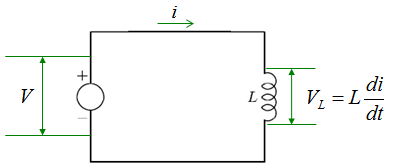
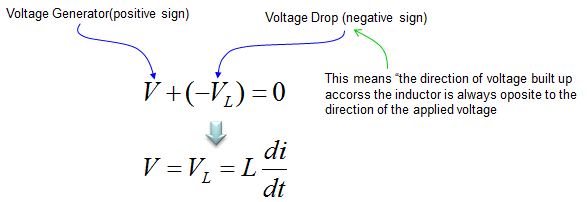
The voltage across an inductor is described as shown below. Since most of the governing equation for electrical component is described in terms of Voltage, I would describe the circuit so as to calculate the voltage across the component. But in some cases you would need to describe the circuit so as to calculate the current or charges. In that case you would need to modify the equation to give you the right form of equation.
Now let's assume that we have a very simple circuit with a Voltage source and an inductor. It can be described as below.
Now let's expand the circuit a little bit further. In this example, We have two components R and L connected in Series and a voltage source to those components as shown below. The governing equation is also based on Kirchoff's law as described below.
The voltage across the resistor and capacitor can be described as shown below. Since most of the governing equation for electrical component is described in terms of Voltage, I would describe the circuit so as to calculate the voltage across the component. But in some cases you would need to describe the circuit so as to calculate the current or charges. In that case you would need to modify the equation to give you the right form of equation.
Applying the Kirchoff's voltage rule, you can combine all the terms shown above into a single equation as shown below. All of these equations mean same thing. In terms of differential equation, the last one is most common form but depending on situation you may use other forms.
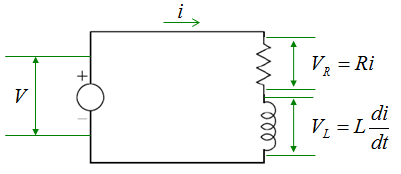
Now We have two components R and L connected in Series and a voltage source to those components as shown below. The governing equation is also based on Kirchoff's law as described below.
The voltage across the resistor and inductor can be described as shown below. Since most of the governing equation for electrical component is described in terms of Voltage, I would describe the circuit so as to calculate the voltage across the component. But in some cases you would need to describe the circuit so as to calculate the current or charges. In that case you would need to modify the equation to give you the right form of equation.
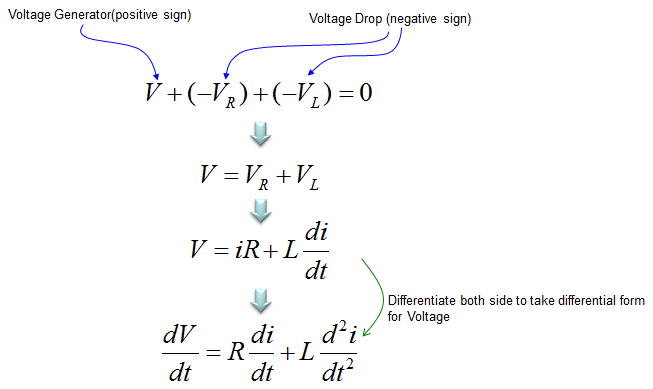
Applying the Kirchoff's voltage rule, you can combine all the terms shown above into a single equation as shown below. All of these equations mean same thing. In terms of differential equation, the last one is most common form but depending on situation you may use other forms.
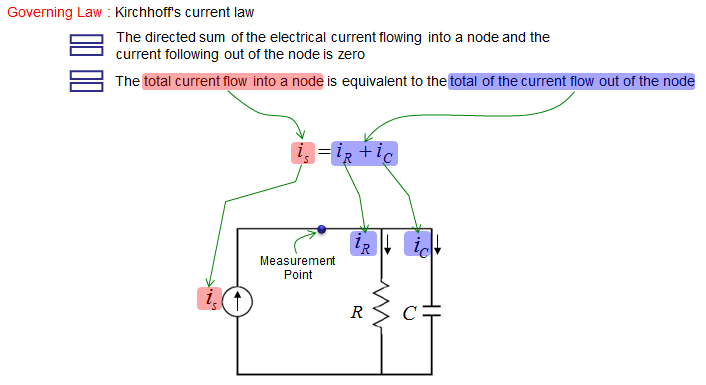
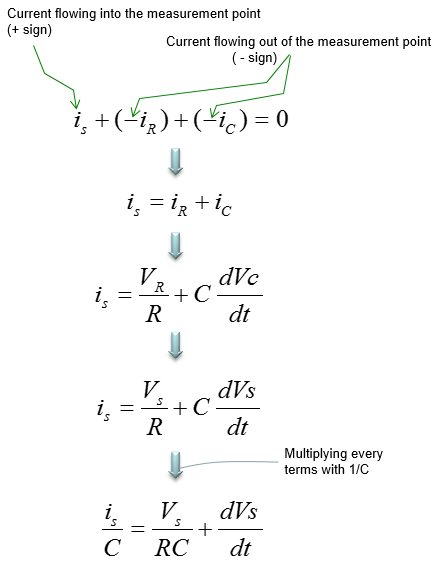
This example is also a circuit made up of R and L, but they are connected in parallel in this example. The governing law of this circuit can be described as shown below.
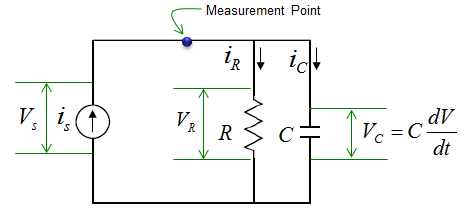
The current through the resistor and capacitor can be described as shown below. Unlike other examples, the governing equation in this example is described in terms of current. The current flowing through each components in the circuit are as shown below.
Applying the governing law for this circuit and with a little bit of rearrangement a differential equation is obtained as follows.
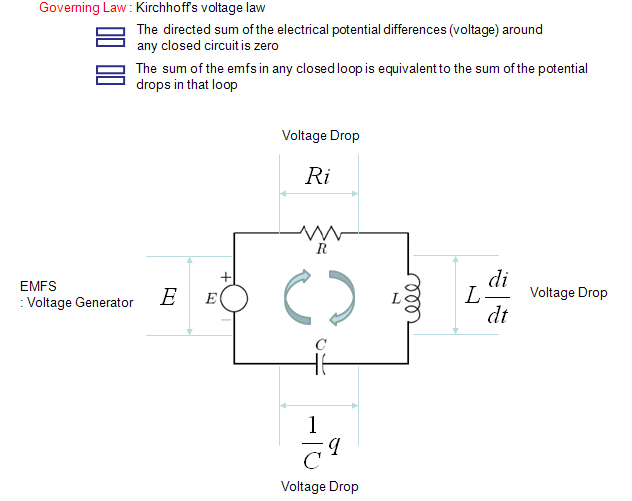
This example shows a circuit that combines R, L, C in series and the governing equation is based on Kirchoff's voltage law.
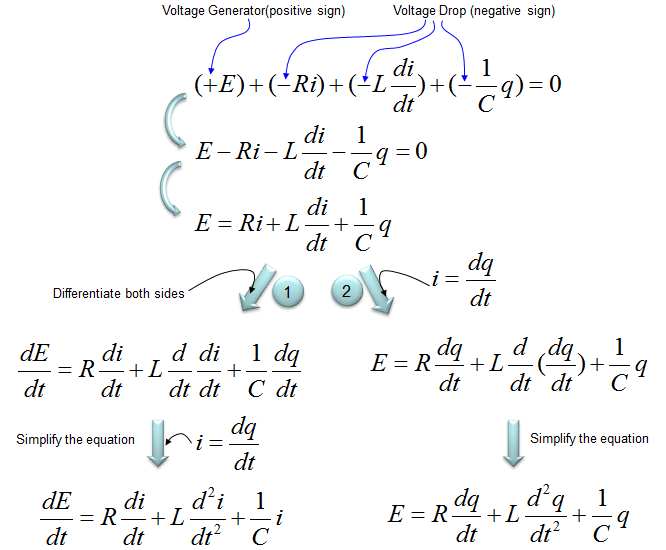
Apllying the governing equation and by some rearrangement, you can derive the differential equation for this system as follows. Depending on which parameter you set it to be the state variable (the paramter to be measured as the output of the system), you can have two different form of the differential equation as shown below. Even though both forms of equation is used in various system modeling, I think the form on the left side would be more frequently used since the variable i (current) can be more easily measured than the variable q (amount of charges). In many cases, the term V is used in stead of E. So replacing E with V may give you the form which you are more familiar with.
|
||