Communication Technology

Delta Function

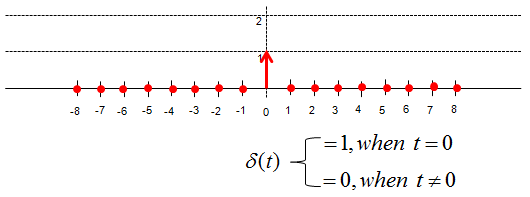
The most important component of signal representation is to understand the meaning of 'delta' fuction. Delta function in discrete signal can be illustrated as below. As you see, delta function is a special function which has '1' only at t = 0 and '0' at all other points. (In case of continuous signal, Delta function is defined as a function where the width of the function is infenitely small and the area under the function is 1).

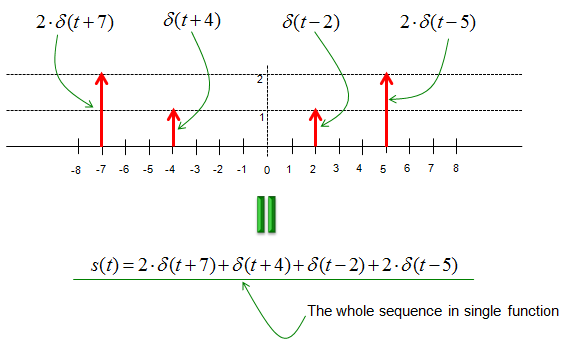
Why do we use this kind of special function ? It is because we can represent any discrete value by shift and multiplication of the function as shown below. (Note : In order for this kind of shift and multiplication to have practical meaning in real application, the system should be LTI (Linear Time Invariant). See Linearity and Time Invariance page.)

If you sum up all of these shift-multiplied versions of delta function, you can even express a sequence of signal in simple mathematical form.

If you want to express the following sequence without using the delta function, you may have to write s(t,x) = {(-8,0),(-7,2),(-6,0),(-5,0),(-4,1),(-3,0),(-2,0),(-1,0),(0,0),(1,0),(2,1),(3,0),(4,0),(5,2),(6,0),(7,0),(8,0)}. You would notice that it is simple to express it in the mathematical form.

Another reason why we use delta function for signal representation is the fact that the characteristics of the delta function is well investigated. Therefore, we can easily identify the characteristics of the signal based on the characteristics of the delta function. (Again, this holds true that the system is Linear Time Invarient).

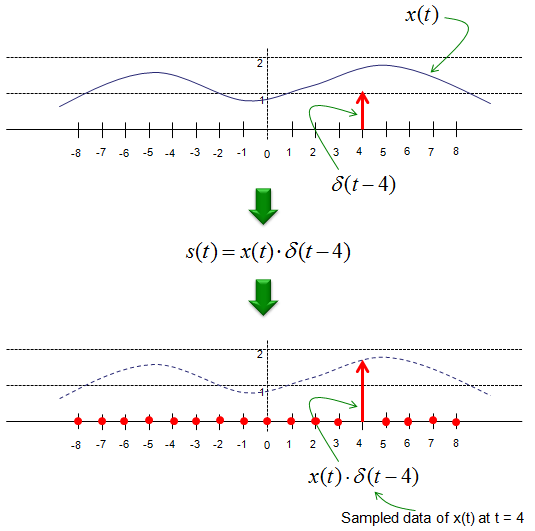
The delta function is also frequently used to represent 'sampling'. Let's say that we have a continuous signal x(t) and we want to express the value of x(t) sampled at t = 4. This can be respresented as shown below. I hope this make sense to you without any further explanation.

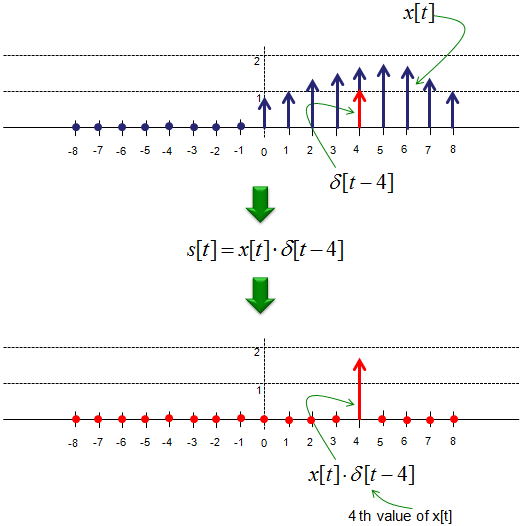
This way of representing the sampling with delta function is also applies to the discrete signal as shown below. Let's say we have a discrete signal x[t] and you want to select out the value at index 4. You can just express it as below.

This kind of mathematical expression may look unnecessarily complicated, but as I mentioned above if you can express your signal into this kind of mathematical form you can easily characterize your signal based on a simple well known signal (delta function). One common example for this is for investigation of the system output for a given input sequence.

For further application of Delta function, refer to Signal Presentation.