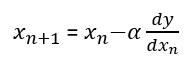Engineering Math - Calculus

Gradient Descent Method

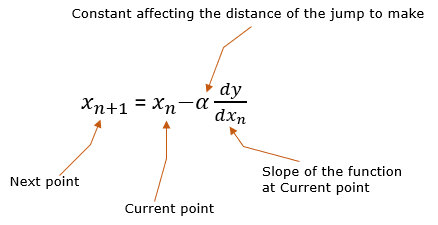
Gradient Descent Method is a technique to find a minimum value of a function by changing the value of variables repeatedly based on the the following rule.

If you can make any sense out of this equation just by looking at this equation, you don't have the read this page any more.

If you still want to get a little bit of further explanation, take a look at following.

Now I hope you got a little bit of more concrete idea, but I think you still want to get some more details. I hope following would help you a little bit further.

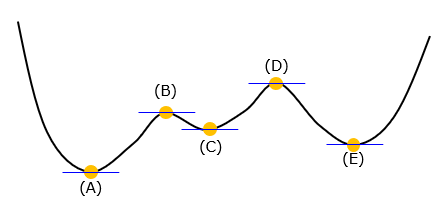
NOTE : At this point, we need to notice a very important point. As mentioned above, the step size (distance of jump) is determined by the constant alpha and the slope of the function (dy/dx). It implies the following two points

    i) if alpha is set to 0, the step size gets 0 meaning the point(x) does not move

    ii) if dy/dx gets 0, the step size gets 0 meaning the point(x) does not move

We don't worry about the point i) because the alpha is completely under our control and we wouldn't set it to zero. The important thing is the point ii). This property acts as a advantage or disadvantage depending on the situation. The minimum position of any continous funtion always have the slope 0 at the point. This is good because this make the point does not move away once it reaches the minimum point. But not every points with the slope 0 is minimum value of the function. For example, let's suppose we have a function as shown below (black curve). In this function graph, you can see 5 position where the slot(dy/dx, gradient) gets 0. If you reach any of these points, you get stuck there (i.e, does not move any more) because the jump size gets 0 due to dy/dx. If you are at (A) and stuck there, it is lucky because it is the real(global) minimum of the function, but if you are at any other points, you get stuck at a wrong point.

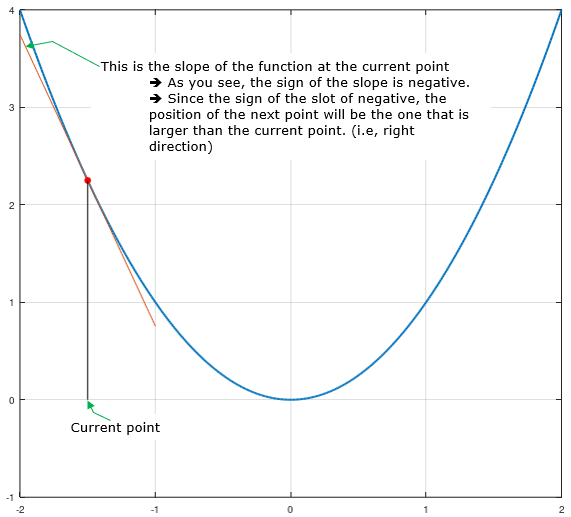
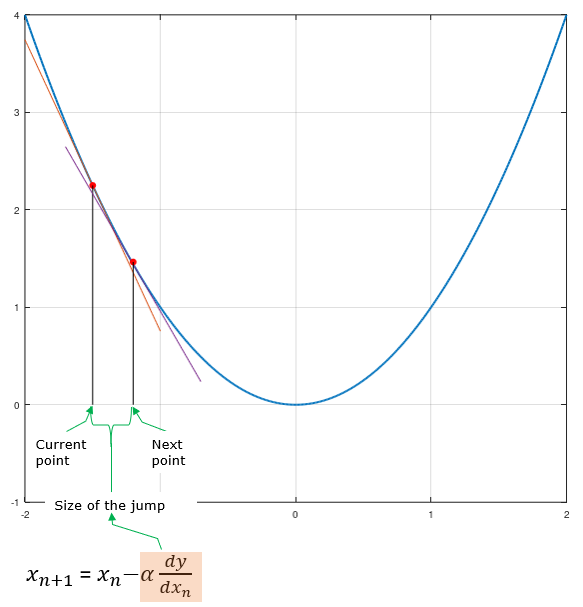
Now let's confirm this explain with a concrete example. Let's assum that you have a quadratic function and you set the initial point as shown below. From this initial point, you have to determine the next point as commented below (try to associate this comments with the mathematical expression shown above).

By this logic, you can get the next point as shown below.

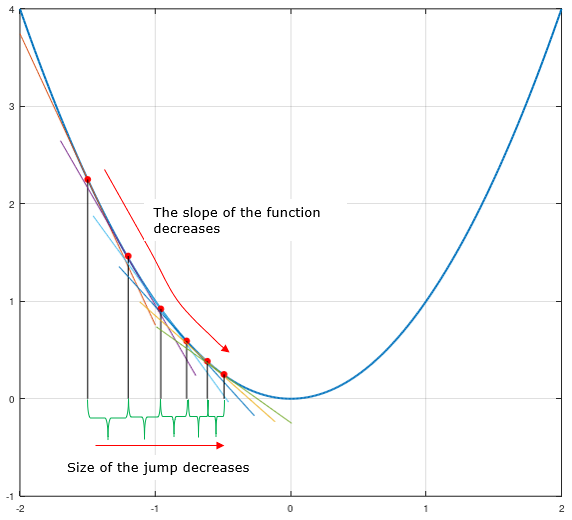
Then from the second point you found, apply the same logic repeatedly until you reach the minimum point of the function. Following plot shows the example of several steps for this function and shows how the slope of the function at each point affects the size of the jump. (NOTE : Click on the graph or here to see the slide show or animation version of this process).

NOTE : Now the last step for you to get the complete understanding is to go through many examples. The best way would be for you to create those examples on your own, but as a second best one I have made those examples for you in slideshow format in my visual note www.slide4math.com . Go to [Engineering]->[2]->[Gradient Descent].

Effect of the Alpha

What I want to talk in this section is about the effect of Alpha in the following equation on the speed of finding the minimum value of a function.

Based on the equation above, the speed of the finding the minimum value is affected by the slope (dy/dx) and the constant alpha. The effect of the slope is briefly described at this NOTE. The effect of Alpha will be explained in this section. In fact, the role of Alpha is much more important in gradient descent algorithm and finding the proper Alpha value in most practical application is not easy.

NOTE : One of the most important application of the Gradient Descent method would be Neural Network. The constant alpha is called Learning Rate and it is very, very important parameter you have to specify properly in Neural Network. What you will learn in this section would be helpful to understand how network parameters (e.g, weights and bias) in Neural Network is calculated and updated.

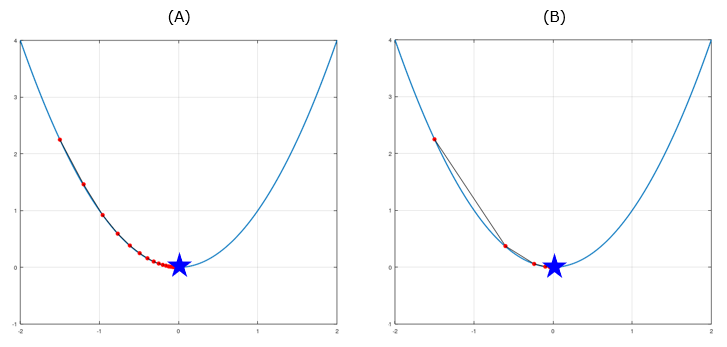
Let's take a look at a simple example as shown below (You can see this example in slideshow in this page in my visual note www.slide4math.com). The goal here is to find the minimum value marked as a blue star and the red dots shows the process of each steps to reach the goal (the black line is connecting the dots of the gradient descent process). The plot (A) and (B) shows the process of gradient descent process with two different Alpha value. (B) uses larger Alpha value than (A).  You see that the large Alpha let you find the min value faster.

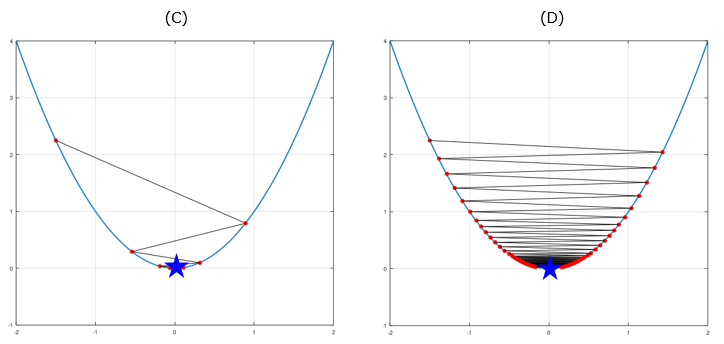
From the above examples, it seems that large Alpha value result in faster min finding. Would this be always true ? Let's increase the Alpha value a little bit further (C) is using the alpha value a little bit larger than the case (B). You see this reaches the min value faster than (A) at least but the path to find the value looks a little strange. Now let's push up the Alpha value further as shown in (D). (D) uses the Alpha value much greater than (C). As you notice here, the path to reach the goal swings back and forth and takes much longer to reach the goal. This example shows simply increasing the Alpha value does not necessarily helps to find the min value quickly.

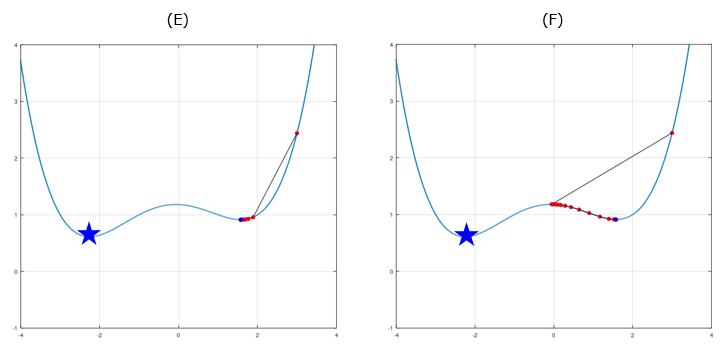
Now let's suppose we have a little bit more complicated function as below. (F) uses larger Alpha then (E), but (F) reaches to 'kind of' min location slower than (E). Note that I said 'kind of' min point.. it is not real min value. The real min value is marked as Star shape. In this case, none of (E) and (F) reaches the real min. (Click here or click on the graph to see this plot in slideshow from www.slide4math.com )

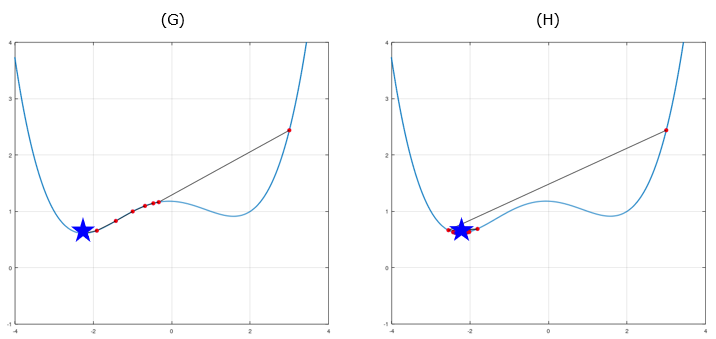
Now let's increase the Alpha a little bit. (G) uses an Alpha larger than (F) and (H) use larger value than (G). (G) barely managed to reach the real min (global min) of the function and (H) reaches the global mean faster than (G). Then let me ask you the same question again. Do you think simply increasing the Alpha value helps finding the global min faster ? Check on your own in this page.

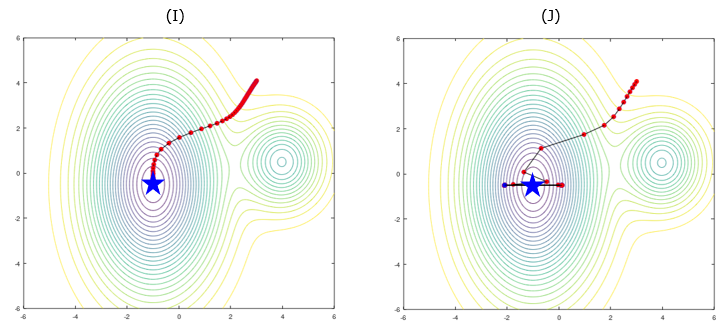
Now let's take a look at a more complicated situation with a case of function of two indepent varaibles. I plot it in a contour plot as shown below. (J) uses the Alpha larger than in (I). In this case, (I) reaches the min value but (J) ends up swinging back and forth between two points (Click here or click on the graph to see this plot in slideshow from www.slide4math.com ).

Based on several examples show above, do you think there is any general rules on the effect of Alpha on the speed of finding the min value.

Unfortunately No. So finding the best Alpha value would be based on more of trial and error.