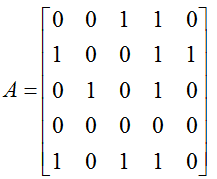Engineering Math - Graph Theory

Dominance

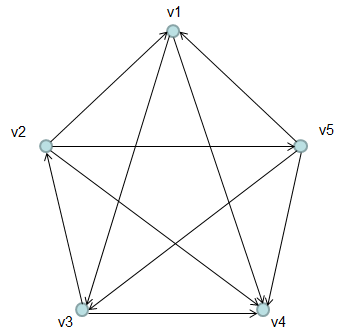
The direction (arrow) in a Graph can be interpreted in many different ways depending on what kind of situation it is representing.

For example, the arrow can represents 'who influence who in a social network'. With this, following graph can be interpreted like this. The member v1 influence v3 and v4. The member v2 influence v1, v4, v5 etc.

The adjacent matrix for this matrix is represented as follows. (If you are not familiar with what Adjacent matrix is, refer to Adjacent Matrix page)

Dominance represents 'who influence the most numbers of other members'. In case of directed graph, it can be identified by 'which vertices has the most numbers of outgoing arrows'.

Dominance among the members can be identified from Adjacent Matrix. You can figure out directly from adjacent matrix itself which vertex is Dominant one in single step.

For example, you can interpret the adjacent matrix as shown below. (In this case, v2 and v3 can be ranked as tie in terms of dominance).

Since we failed to find single dominant element from Adjacent matrix, we can check with the second step relationship by taking the power of 2 for the adjacent matrix. The result can be illustrated as follows.

If you sum up both the first step dominance and the second step dominance, you will have the matrix as follows. From this matrix, you can identify a single, the most dominant member.