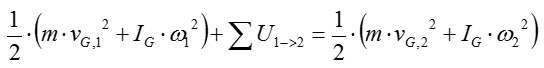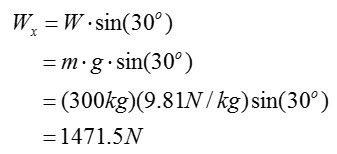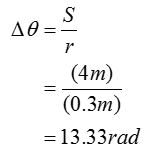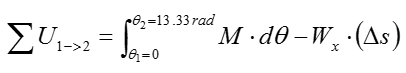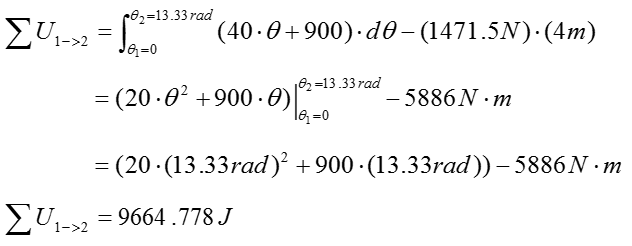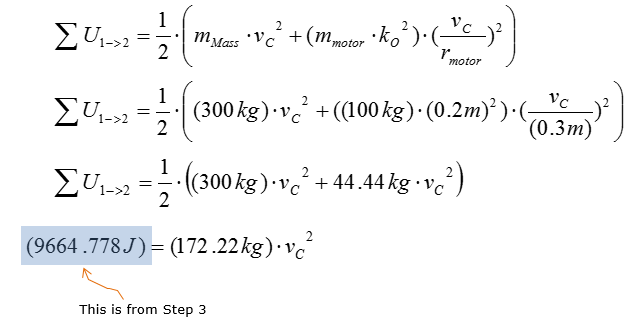|
Mechanical Engineering |
||
|
Work by Couple Moment
Example 01 >
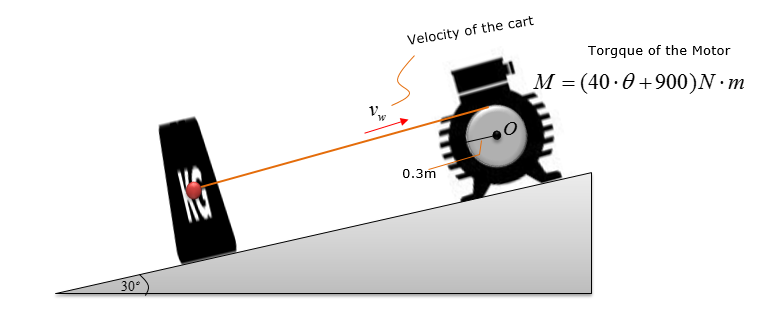
The wheel with a mass of 100 kg and a radius of gyration of ko = 0.2 m is connected to a motor. The motor supplies a torque M = (40 th + 900) N m , where th is in radians around the drive shaft at O. Determine the speed of the loading car, which has a mass of 300kg, after it travels s = 4m. Initially the car is at rest when s = 0 and th = 0 . Neglect the mass of the attached cable and the friction between the mass and the surface.
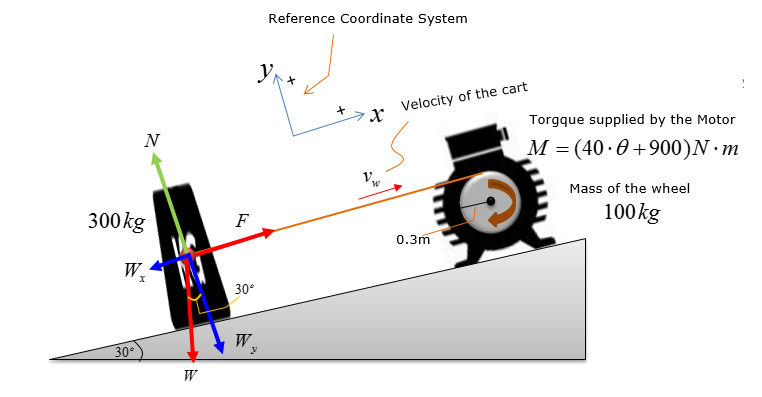
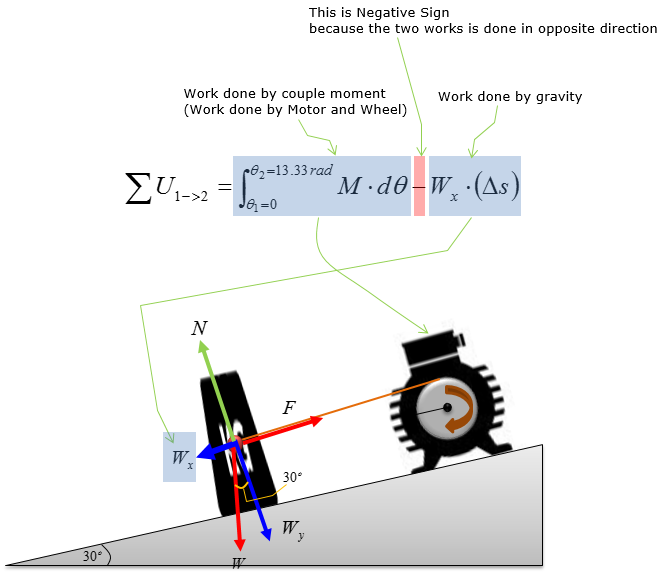
Step 1 > Draw Free Body Diagram
The first step of solving any kind of Dynamics problem would be to draw Free Body Diagram and put all the known information on the figure of the problem.
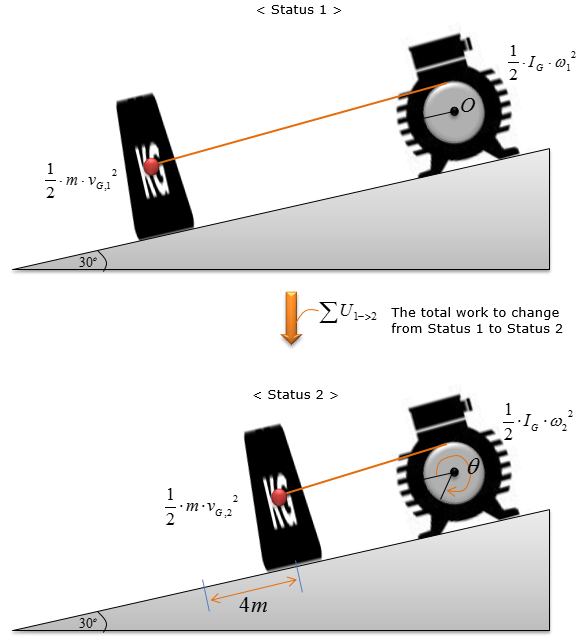
Step 2 > Situational analysis and simplifying the problem
Principle of work and energy is the governing equation for calculating the resultant velocity of the cart since its displacement is known, which is 4m. This can be illustrated as below.
This illustration can be expressed in the energy equation as shown below (It is assumed that the motor and mass are at rest (i.e, not moving)).
Since the system is initially at rest, the initial kinetic energy equals zero. Therefore, the engergy and work equation can be simplified as below
Analyze the forces on the cart and compute the expression for each forces. Observing the free-body-diagram of the cart, F does work on the cart, while Wx does work against the cart. Assume frictionless surface as the coefficient of friction is not given. Compute the expressions for F and Wx.
Consider Wx.
Wx will be used to calculate the work done against the Mass.
Consider F.
Since the force F on the Mass is generated by the applied moment (M) from the motor, the work done by F will be calculated using the couple moment energy equation, which states that the applied work corresponds to the product of applied moment and angular displacement of the motor.
Compute the angular displacement of the motor. It must be in radians to calculate work done by couple moment as the given moment is in Nm, which is equivalent to J.
It is given that the total distance traveled by the coupling on the winding motor (S) = 4 m
With the displacement and radius of the wheel, the total angular displacement of the motor wheel can be calculated as follows
< Step 3 > Calculate the work done on the cart
The detailed meaning of this equation can be illustrated below (If you can understand this equation without looking into following illustration, you already have good understanding on the system analysis)
Now just do the simple math, you can calculate the amount of the work as follows.
Step 4 > Calculate the velocity of the cart at s = 4m
Consider the resultant kinetic energy of the cart. Since the motor and cart are connected as one system, the velocity of the cart is affected by the rotation of the motor. Since mass moment of inertia is induced in the motor, adding rotational resistance, the final kinetic energy of the cart is equal to the sum of kinetic energy of the cart and kinetic energy of the motor due to inertia. As a result, the change in velocity of the cart is lowered. The linear velocity of the motor at r = 0.3m is equal to the velocity of the cart, as they are connected as one system.
Looking back to < Step 2 >, we have the following equation.
From this, you can figure out the velocity of the Mass at the displacement of 4 m as follows.
Reference
|
||