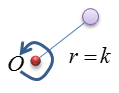Mechanical Engineering

Radius of Gyration

The meaning of 'Gyration' is 'Rotation (Circular Motion)'. Therefore, 'Radius of Gyration' mean 'Radius of Rotation'. It may sound easy .. but what does it really mean ? Then you would find it not easy to answer the question in nice and easy way. To be honest, I also don't have much nicer way to describe 'Radious of Gyration' verbally, but I think I can help you to have some intuitive understanding on this concept.

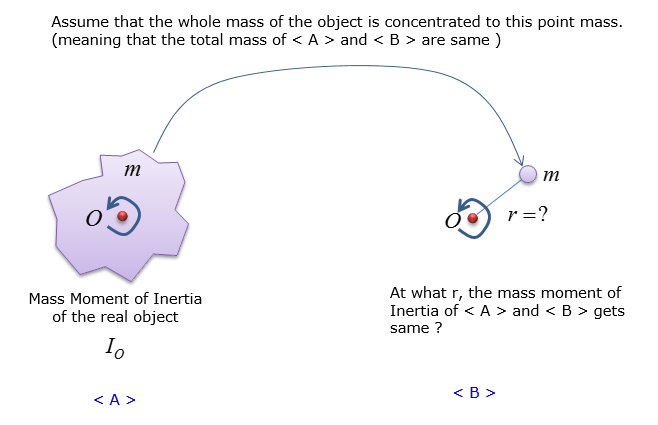
Let's suppose that you have an object as shown in < A >.  If you rotate this object at a point O, you would know that the movement of the object can be explained by Mass Moment of Inertia. It would not be easy to calculate the Mass Moment of Inertia of this kind of arbitrary shaped object, but let's just assume that you know the Mass Moment of Inertia for this object (Let's call the Mass Moment of Inertia for this object as Io).

Now let's assume that you can squeeze the object <A> into a small point mass as shown in <B>. And then you connect a thin string to the point mass and rotate it. The moment of inertia for the point mass would vary depending on the length of the string (i.e, the radius of the rotation).

Now let me ask you a quetion. What is the length of the string (i.e, the radius of the rotation) that make the mass moment of inertia of < B > equal to the mass of inertia of <A> ?

If you get the value (let's call the number as k), it is 'Radius of Gyration' of the object <A>.

Now let's assume that you have figured out the Radius of Gyration (k) of the object < A >.  Then, the rotating system can be simplified as an imaginary rotating mass shown below.

Then from this, you can calculate the mass moment of inertia of the object <A> using the Radius of Gyration as shown below.

Reference

[1] Radius of Gyration and Buckling (YouTube)

[2] Visualizing Mechanics: Radius of Gyration (YouTube)