|
Matlab Toolbox - Machine Learning |
||
|
Patternnet
This example is almost same as what I showed you in feedforwardnet. In terms of the structure of the network, I don't see any difference between feedforwardnet and Patternent. But it seems there is a slight difference in terms of the training parameters between the two since I am getting slightly different result. I am not sure exactly what is the difference between the two. What I am trying to show is that there are multiple ways to do the same (or similar) things.
Hidden Layer Size : 7 Perceptrons
In this example, I will try to classify this data using two layer network : 7 perceptrons in the Hidden layer and one output perceptron. Let's see how well this work. The basic logic is exactly same as in previous section. The only difference is that I have more cell(perceptron) in the hidden layer. What do you think ? Would it give a better result ? If it give poorer result, would it be because of this one additional cell in the hidden layer ? or would it be because other training parameters are not optimized properly.
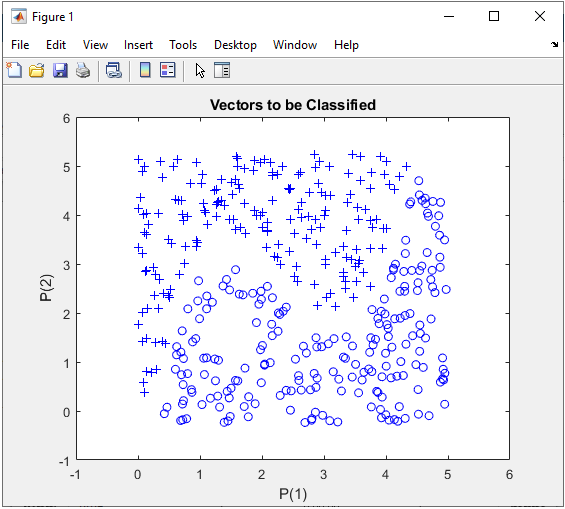
Step 1 : Take a overall distribution of the data plotted as below and try to come up with some idea what kind of neural network you can use. I use the following code to create this dataset. It would not be that difficult to understand the characteristics of dataset from the code itself, but don't spend too much time and effort to understand this part. Just use it as it is.
full_data = [];
xrange = 5; for i = 1:400
x = xrange * rand(1,1); y = xrange * rand(1,1);
if y >= 0.6 * (x-1)*(x-2)*(x-4) + 3 y = y + 0.25; z = 1; else y = y - 0.25; z = 0; end
full_data = [full_data ; [x y z]];
end
In this case, only two parameters are required to specify a specific data. That's why you can plot the dataset in 2D graph. Of course, in real life situation this would not be a frequent case where you can have this kind of simple dataset, but I would recommend you to try with this type of simple dataset with multiple variations and understand exactly what type of variation you have to make in terms of neural network structure to cope with those variations in data set.
Step 2 : Determine the structure of Neural Nework.
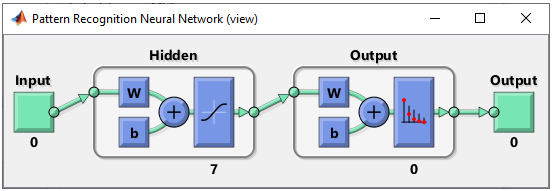
The structure of the network I want to buil is as below. You see there is 7 neurons in Hidden layer. But you would notice that the number of neuron is 0 at the output. This is not what I want. However, as in feedforwardnet, patternnet automatically configures output layer structure from the training set data structure. So it shows the number of output neuron as 0 before you run train() function.
This structure can be created by following code. Compare this with perceptron network case for the same network shown here and see how simpler it is to use feedforwardnet() function. Basically it is just one line of code to create the network and additional lines after feedforwardnet() is to change some parameters. If you want to use the default parameters, you don't need to add those additional lines. net = patternnet(7); % NOTE : the number 7 here indicate the number of neurons in the first layer % (i.e, the hidden layer in the whole network). You don't need to specify Output % layer because it is automatically set by the output data you are poassing in % train() function.
In this example, I didn't set any additional properties of the network and just use the detaulf settings of patternnet() function.
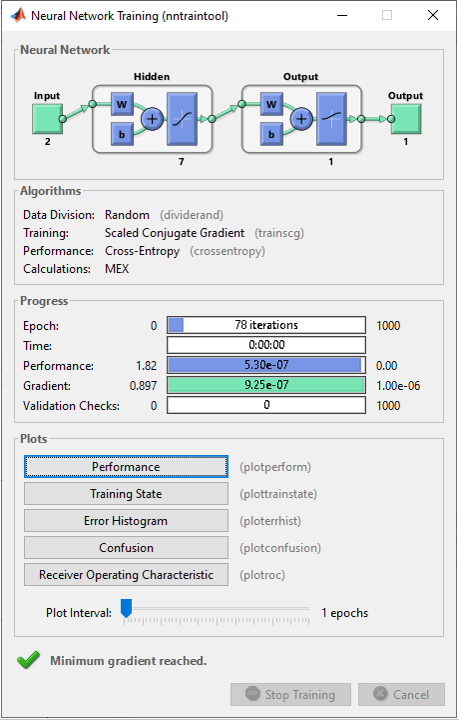
Step 3 : Train the network. Training a network is done by a single line of code as follows. [net,tr] = train(net,pList,tList); I didn't set any properties of train() function in this example and wanted to see how well the default setting works.
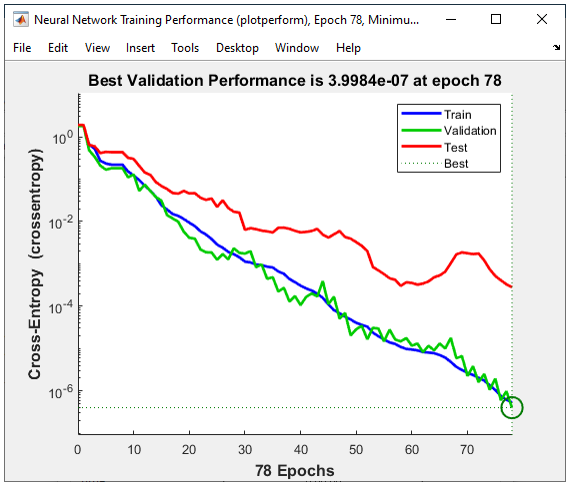
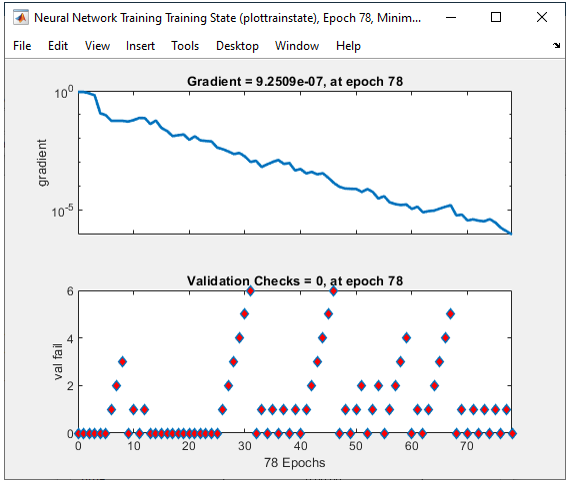
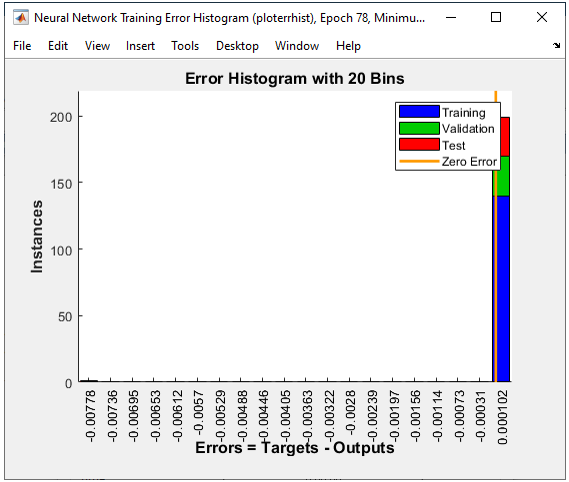
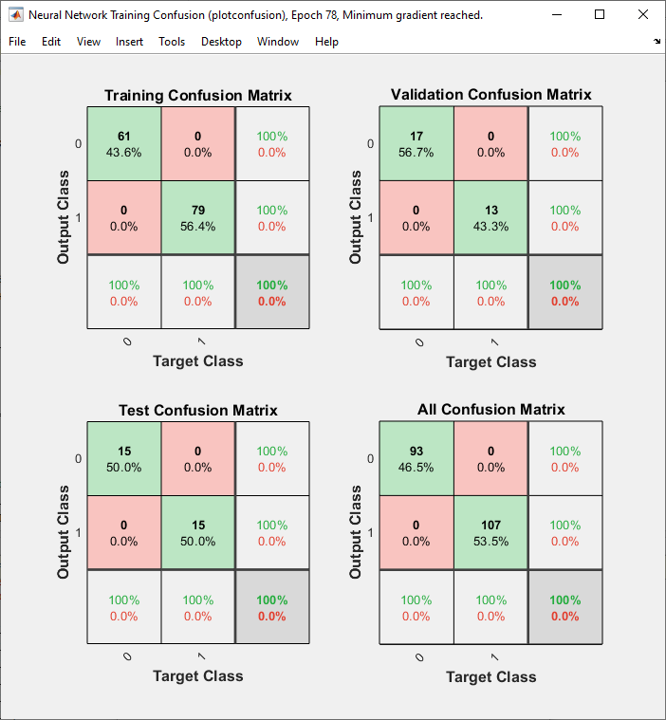
The result in this example is as shown below.
NOTE : Now you see the number of neurons in Outpu layer is shown as non zero which is determined automatically from output data structure (tList in train() function in this example). The type of activation function in the output layer is also changed automatically based on tList data structure.
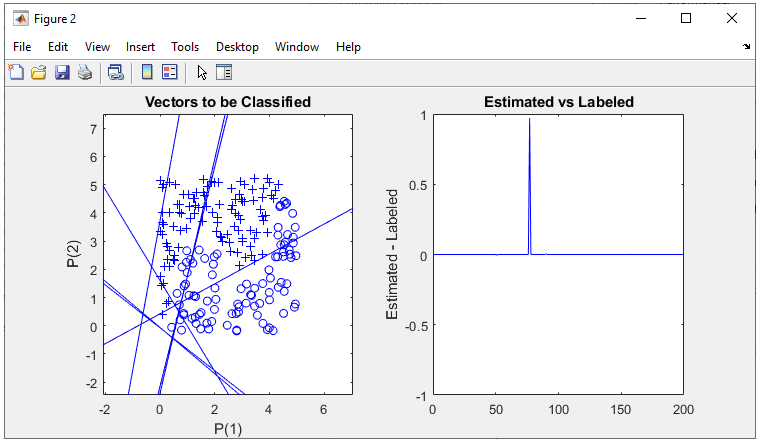
As shown below, the performance is similar to the perceptron network with the same same number of neurons in each layer.
All of the following plots are showing how the training process reaches the target at each iteration. I would not explain on these plots.
Next Step :
|
||