Python

  

 

 

 

Cluster - pyTorch

 

In this note, I want to try to apply an approach that is completely from other notes. I wanted to use chatGPT to create a Python code that I want instead of writing it myself.

 

NOTE : Refer to this note for my personal experience with chatGPT coding and advtantage & limitation of the tool. In general, I got very positive impression with chatGPT utilization for coding.

 

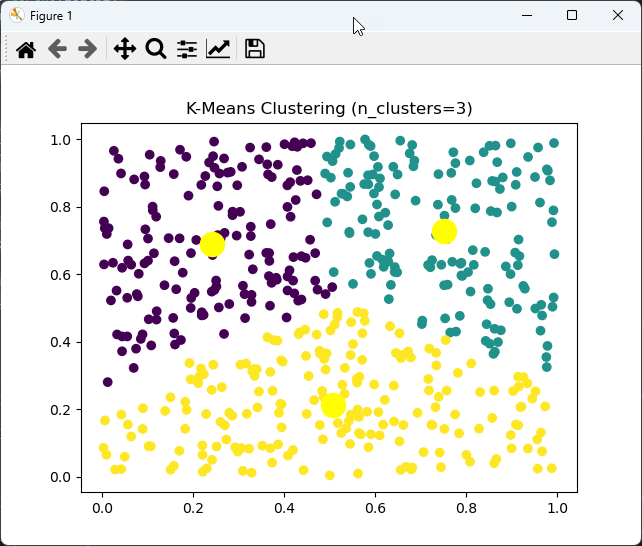
This code is created first by chatGPT on Feb 03 2023 (meaning using chatGPT 3.5). For this code, I haven't started from the requirement. I asked chatGPT to write the same function as this using pyTorch.

 

As you notice, this code uses some math function of torch, but does not use any neural net.

 

NOTE : To my surprise (in negative way), chatGPT coding was a little bit disappointing in terms of pyTorch coding. It seems chatGPT became dumb. In most case, the initial response was the code with syntax errors and when I said 'fix it' it rewrite the entire code in complete different way instead of the fixing a specific part and the new code generates other syntax error. At first, I thought chatGPT would write stable, high quality Python code because I assumed that it has been trained most extensively for Python because I thought there are the most amount of python code shared by gitHub or stackoverflow etc.

 

Cluster_kCluster_PyTorch_01.py

import torch

import matplotlib.pyplot as plt

 

def kmeans(data, n_clusters, n_init=10, max_iter=300, tol=0.0001, random_state=0):

 

    data = torch.tensor(data, dtype=torch.float32)

    num_points, num_dims = data.shape

 

    # initialize cluster centroids randomly

    centroids = data[torch.randperm(num_points)[:n_clusters]]

 

    for i in range(max_iter):

        # calculate distances between each point and the centroids

        distances = torch.stack([((data - centroids[j])**2).sum(dim=1) for j in range(n_clusters)])

 

        # find the closest centroid for each data point

        closest_centroids = distances.argmin(dim=0)

 

        # update the centroids to be the mean of the data points assigned to them

        new_centroids = torch.stack([data[closest_centroids == j].mean(dim=0) for j in range(n_clusters)])

 

        # check if the centroids have changed

        if (new_centroids - centroids).abs().max() < tol:

            break

        centroids = new_centroids

 

    return closest_centroids, centroids

 

def display_result(X, y_pred, n_clusters, centroids):

    X = torch.tensor(X, dtype=torch.float32)

    plt.scatter(X[:, 0], X[:, 1], c=y_pred)

    plt.scatter(centroids[:, 0], centroids[:, 1], s=300, c='yellow', label='Centroids')

    plt.title(f'K-Means Clustering (n_clusters={n_clusters})')

    plt.show()

 

def test_kmeans():

    # Generate random sample data with 100 samples and 2 features

    n_samples = 500

    n_features = 2

    X = torch.rand(n_samples, n_features).numpy()

    n_clusters = 3

 

    # Call the kmeans function

    labels, centroids = kmeans(X, n_clusters)

 

    # Assert that the shape of the labels is correct

    assert labels.shape == (n_samples,), f"Expected shape {(n_samples,)}, but got {labels.shape}"

 

    # Assert that the shape of the centroids is correct

    assert centroids.shape == (n_clusters, n_features), f"Expected shape {(n_clusters, n_features)}, but got {centroids.shape}"

 

    # Display the result

    display_result(X, labels, n_clusters, centroids)

 

test_kmeans()

 

 

The result from this code is as follows :

 

 

 

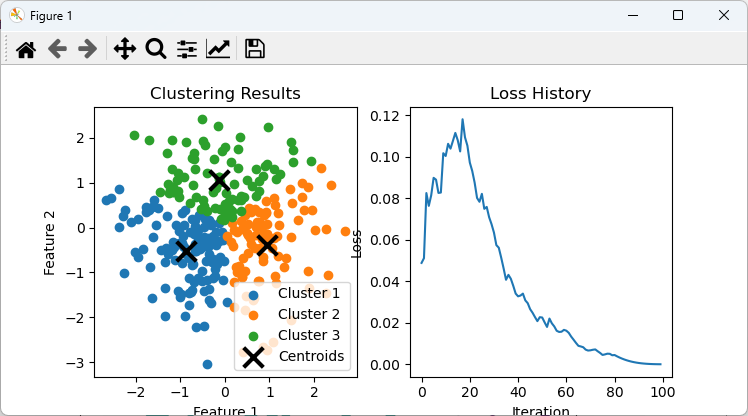
I asked chatGPT to use 'feedforward neural net' and got the same code and plot clustered output and loss values in the same figure.

 

NOTE : I expected a little bit different code from this. I expected chatGPT to use multiple layers of linear layers but the result is not what I expected. Probably the term 'feedforward' in my request was interpreted differently. But the outcome of the execution is exactly what I wanted get.

 

Cluster_kCluster_PyTorch_NN_01.py

import torch

import torch.nn as nn

import torch.optim as optim

import numpy as np

import matplotlib.pyplot as plt

 

def k_means_clustering_nn(X, n_clusters, n_iter=100):

    X = torch.tensor(X, dtype=torch.float32)

    n_samples, n_features = X.shape

    centroids = torch.randn((n_clusters, n_features), dtype=torch.float32)

    cluster_assignment = torch.zeros((n_samples,), dtype=torch.int64)

    loss_hist = []

 

    class KMeansClusteringNN(nn.Module):

        def __init__(self):

            super(KMeansClusteringNN, self).__init__()

            self.centroids = nn.Parameter(torch.randn((n_clusters, n_features), dtype=torch.float32))

    

        def forward(self, X):

            X = X.unsqueeze(1)

            distances = (X - self.centroids)**2

            distances = torch.sum(distances, dim=2)

            cluster_assignment = torch.argmin(distances, dim=1)

            return cluster_assignment

 

    model = KMeansClusteringNN()

    optimizer = optim.Adam(model.parameters(), lr=1e-2)

    for i in range(n_iter):

        optimizer.zero_grad()

        cluster_assignment = model(X)

        loss = 0

        for c in range(n_clusters):

            points_in_cluster = X[cluster_assignment == c]

            mean_of_points = torch.mean(points_in_cluster, dim=0)

            centroids_loss = torch.sum((mean_of_points - model.centroids[c])**2)

            loss += centroids_loss

        loss /= n_clusters

        loss.backward()

        optimizer.step()

        loss_hist.append(loss.item())

    

    with torch.no_grad():

        final_cluster_assignment = model(X)

        final_centroids = model.centroids.detach().numpy()

    

    return final_centroids, final_cluster_assignment.numpy(), loss_hist

 

# generate sample data

np.random.seed(0)

X = np.random.randn(300, 2)

n_clusters = 3

centroids, cluster_assignment, loss_hist = k_means_clustering_nn(X, n_clusters)

 

 

fig, ax = plt.subplots(1, 2, figsize=(12, 4))

 

# plot clustering results

for c in range(n_clusters):

    points_in_cluster = X[cluster_assignment == c]

    ax[0].scatter(points_in_cluster[:, 0], points_in_cluster[:, 1], label=f'Cluster {c+1}')

ax[0].scatter(centroids[:, 0], centroids[:, 1], marker='x', color='k', s=200, linewidth=3, label='Centroids')

ax[0].set_xlabel('Feature 1')

ax[0].set_ylabel('Feature 2')

ax[0].set_title('Clustering Results')

ax[0].legend()

 

# plot loss history

ax[1].plot(loss_hist)

ax[1].set_xlabel('Iteration')

ax[1].set_ylabel('Loss')

ax[1].set_title('Loss History')

 

plt.show()

 

 

 

The result from this code is as follows :