|
|
||
|
nn.Sequential is a module that can pack multiple components into a complicated or multilayer network.
NOTE : The Pytorch version that I am using for this tutorial is as follows. >>> print(torch.__version__) 1.0.1 Creating a FeedForwardNetwork : 1 Layer
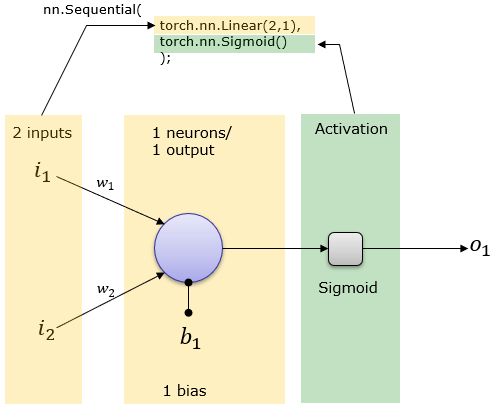
To use nn.Sequential module, you have to import torch as below. import torch2 Inputs , 1 outputs and Activation Functionnet = torch.nn.Sequential( torch.nn.Linear(2,1), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
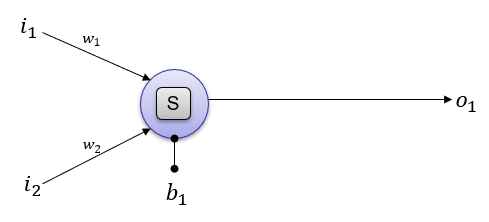
The above illustration would be easier to map between Pytorch code and network structure, but it may look a little bit different from what you normally see in the textbook or other documents. It can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=2, out_features=1, bias=True) (1): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Network Structure of the first component :\n',net[0]) print('Weight of network :\n',net[0].weight) print('Bias of network :\n',net[0].bias) ==> Network Structure of the first component : Linear(in_features=2, out_features=1, bias=True) Weight of network : Parameter containing: tensor([[-0.6538, -0.2817]], requires_grad=True) Bias of network : Parameter containing: tensor([0.0853], requires_grad=True) You can get access to the second component as follows. print('Activation function of network :\n',net[1]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.2994]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.2994]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4698]], grad_fn=<SigmoidBackward>)
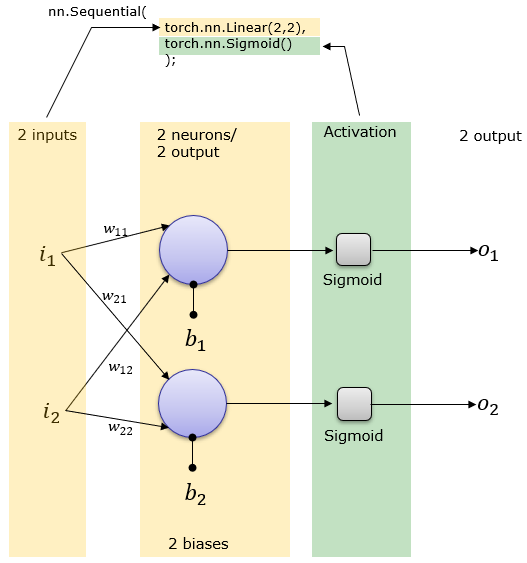
o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4698]], grad_fn=<SigmoidBackward>) 2 Inputs , 2 outputs and Activation Functionnet = torch.nn.Sequential( torch.nn.Linear(2,2), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
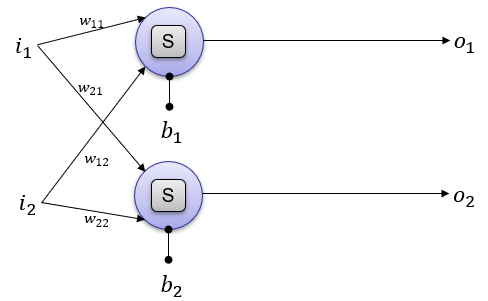
The above illustration can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=2, out_features=2, bias=True) (1): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Network Structure of the first component :\n',net[0]) print('Weight of network :\n',net[0].weight) print('Bias of network :\n',net[0].bias) ==> Network Structure of the first component : Linear(in_features=2, out_features=2, bias=True) Weight of network : Parameter containing: tensor([[ 0.5693, -0.2468], [ 0.5108, -0.7040]], requires_grad=True) Bias of network : Parameter containing: tensor([-0.4882, 0.3872], requires_grad=True) You can get access to the second component as follows. print('Activation function of network :\n',net[1]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]]) print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4587, 0.5484]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4587], [0.5484]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.3648, 0.5216]], grad_fn=<SigmoidBackward>)
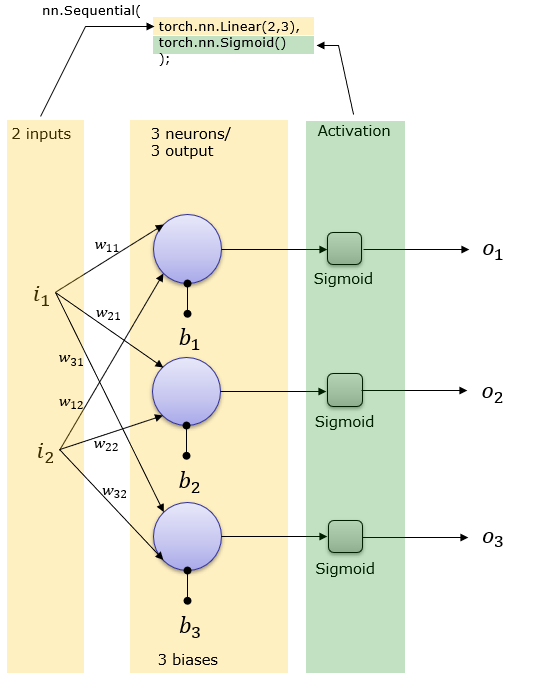
o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.3648], [0.5216]], grad_fn=<SigmoidBackward>) 2 Inputs , 3 outputs and Activation Functionnet = torch.nn.Sequential( torch.nn.Linear(2,3), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
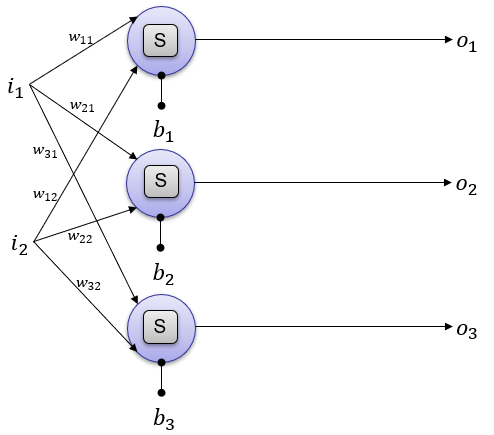
The above illustration can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=2, out_features=3, bias=True) (1): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Network Structure of the first component :\n',net[0]) print('Weight of network :\n',net[0].weight) print('Bias of network :\n',net[0].bias) ==> Weight of network : Linear(in_features=2, out_features=3, bias=True) Bias of network : Parameter containing: tensor([[-0.4764, 0.3788], [ 0.0282, -0.0915], [ 0.4938, 0.5677]], requires_grad=True) Bias of network : Parameter containing: tensor([-0.2263, -0.0468, -0.4945], requires_grad=True) You can get access to the second component as follows. print('Activation function of network :\n',net[1]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4197, 0.4725, 0.6381]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4197], [0.4725], [0.6381]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4789, 0.4776, 0.4598]], grad_fn=<SigmoidBackward>)
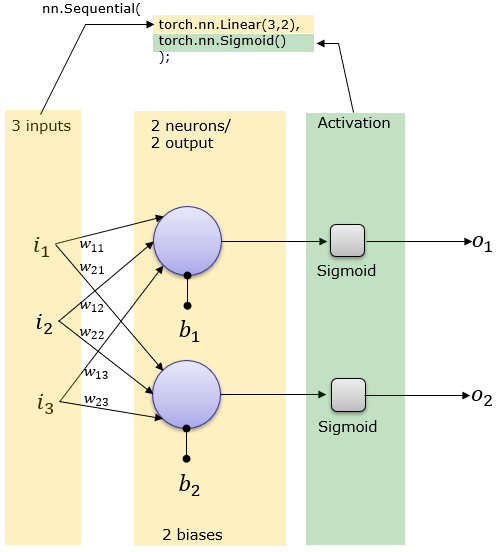
o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4789], [0.4776], [0.4598]], grad_fn=<SigmoidBackward>) 3 Inputs , 2 outputs and Activation Functionnet = torch.nn.Sequential( torch.nn.Linear(3,2), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
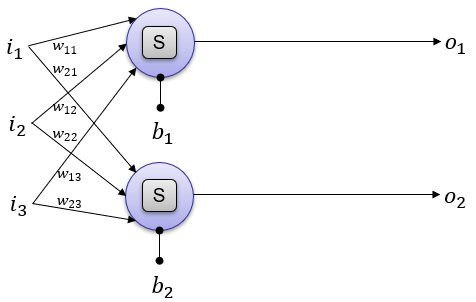
The above illustration can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=3, out_features=2, bias=True) (1): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Network Structure of the first component :\n',net[0]) print('Weight of network :\n',net[0].weight) print('Bias of network :\n',net[0].bias) ==> Weight of network : Linear(in_features=3, out_features=2, bias=True) Bias of network : Parameter containing: tensor([[-0.1829, 0.3458, -0.2496], [-0.5103, 0.0321, 0.3386]], requires_grad=True) Bias of network : Parameter containing: tensor([-0.2709, -0.4960], requires_grad=True) You can get access to the second component as follows. print('Activation function of network :\n',net[1]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1., 1.]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4115, 0.3462]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4115], [0.3462]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000, 1.0000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.4095, 0.4521]], grad_fn=<SigmoidBackward>)
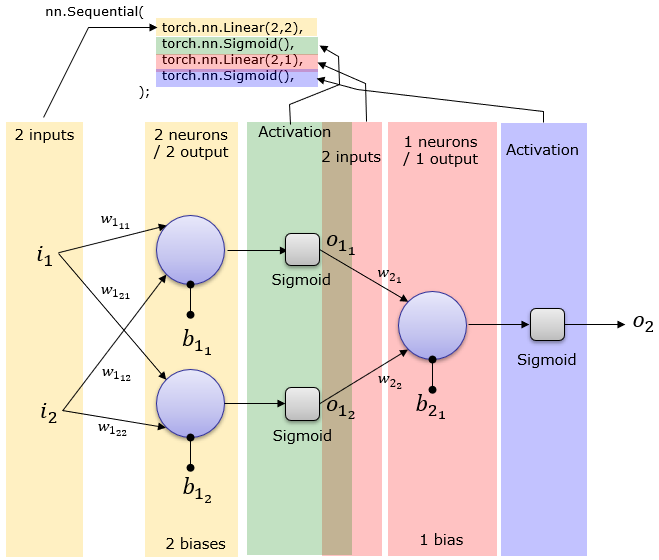
o = torch.mm(net[0].weight,x.t()) + net[0].bias; print('Sigmoid(w x + b) :\n',torch.nn.Sigmoid().forward(o)) ==> Sigmoid(w x + b) : tensor([[0.4095], [0.4521]], grad_fn=<SigmoidBackward>) Creating a FeedForwardNetwork : 2 LayerTo use nn.Sequential module, you have to import torch as below. import torch 1 Hidden Layer : 2 neuron, 1 Output Layernet = torch.nn.Sequential( torch.nn.Linear(2,2), torch.nn.Sigmoid() torch.nn.Linear(2,1), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
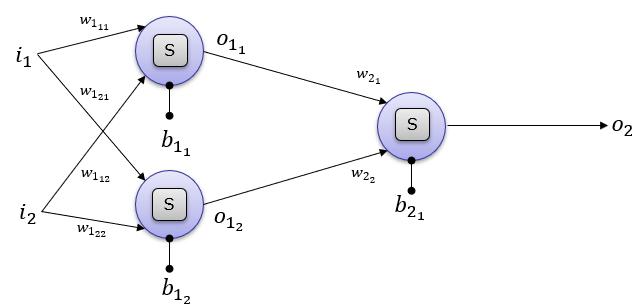
The above illustration can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> Sequential( (0): Linear(in_features=2, out_features=2, bias=True) (1): Sigmoid() (2): Linear(in_features=2, out_features=1, bias=True) (3): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Structure of network net[0] :\n',net[0]) print('Weight of network net[0] :\n',net[0].weight) print('Bias of network net[0] :\n',net[0].bias) ==> Structure of network net[0] : Linear(in_features=2, out_features=2, bias=True) Weight of network net[0] : Parameter containing: tensor([[ 0.1100, 0.5608], [-0.3280, 0.4901]], requires_grad=True) Bias of network net[0] : Parameter containing: tensor([ 0.2237, -0.3034], requires_grad=True) You can get access to the second component as follows. print('Activation function of network net[0] :\n',net[1]) ==> Sigmoid() Now you can get access to next layer (output layer) as below. print('Structure of network net[2] :\n',net[2]) print('Weight of network net[2] :\n',net[2].weight) print('Bias of network net[2] :\n',net[2].bias) ==> Structure of network net[2] : Linear(in_features=2, out_features=1, bias=True) Weight of network net[2] : Parameter containing: tensor([[ 0.1187, -0.4156]], requires_grad=True) Bias of network net[2] : Parameter containing: tensor([-0.4141], requires_grad=True) You can get access to the second component as follows. print('Activation function of network net[2] :\n',net[3]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.3635]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o1 = torch.mm(net[0].weight,x.t()) + net[0].bias.view(2,1); o1 = torch.nn.Sigmoid().forward(o1).t(); o2 = torch.mm(net[2].weight,o1.t()) + net[2].bias; o2 = torch.nn.Sigmoid().forward(o2); print('Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) :\n',o2) ==> Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) : tensor([[0.3635]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.3569]], grad_fn=<SigmoidBackward>)
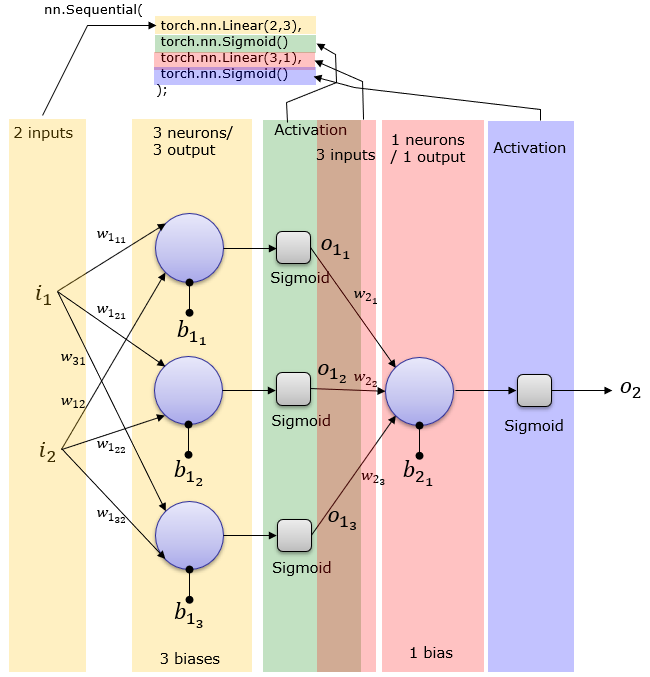
o1 = torch.mm(net[0].weight,x.t()) + net[0].bias.view(2,1); o1 = torch.nn.Sigmoid().forward(o1).t(); o2 = torch.mm(net[2].weight,o1.t()) + net[2].bias; o2 = torch.nn.Sigmoid().forward(o2); print('Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) :\n',o2) ==> Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) : tensor([[0.3569]], grad_fn=<SigmoidBackward>) 1 Hidden Layer : 3 neuron, 1 Output Layernet = torch.nn.Sequential( torch.nn.Linear(2,3), torch.nn.Sigmoid() torch.nn.Linear(3,1), torch.nn.Sigmoid() ); This creates a network as shown below. Weight and Bias is set automatically.
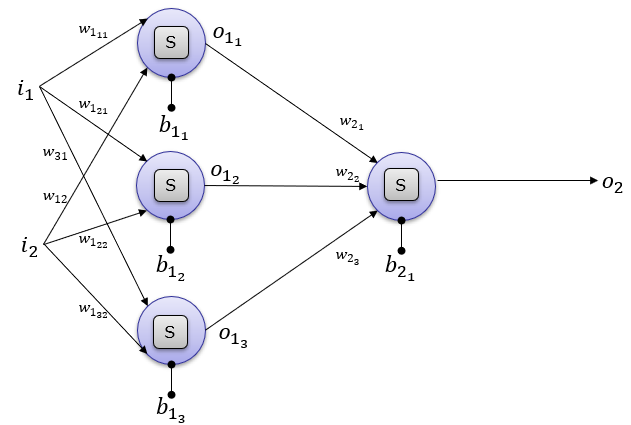
The above illustration can be converted to a little bit different form that is used more often in neural network documents. [S] in the following illustration indicates the Sigmoid activation function.
You can print out overal network structure and Weight & Bias that was automatically set as follows. print('network structure :\n',net) ==> Sequential( (0): Linear(in_features=2, out_features=3, bias=True) (1): Sigmoid() (2): Linear(in_features=3, out_features=1, bias=True) (3): Sigmoid() ) You can get access to each of the component in the sequence using array index as shown below. print('Structure of network net[0] :\n',net[0]) print('Weight of network net[0] :\n',net[0].weight) print('Bias of network net[0] :\n',net[0].bias) ==> Structure of network net[0] : Linear(in_features=2, out_features=3, bias=True) Weight of network net[0] : Parameter containing: tensor([[-0.3463, 0.1359], [ 0.6158, 0.3337], [ 0.4420, 0.4636]], requires_grad=True) Bias of network net[0] : Parameter containing: tensor([-0.5370, -0.5535, 0.3774], requires_grad=True You can get access to the second component as follows. print('Activation function of network net[0] :\n',net[1]) ==> Sigmoid() Now you can get access to next layer (output layer) as below. print('Structure of network net[2] :\n',net[2]) print('Weight of network net[2] :\n',net[2].weight) print('Bias of network net[2] :\n',net[2].bias) ==> Structure of network net[2] : Linear(in_features=3, out_features=1, bias=True) Weight of network net[2] : Parameter containing: tensor([[ 0.3396, -0.4236, -0.4387]], requires_grad=True) Bias of network net[2] : Parameter containing: tensor([0.5372], requires_grad=True) You can get access to the second component as follows. print('Activation function of network net[2] :\n',net[3]) ==> Sigmoid() You can evaluate the whole network using forward() function as shown below. x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.5124]], grad_fn=<SigmoidBackward>) You can evaluate the network manually as shown below. This manual test can be dual purposed. One is to verify the result of forward() function and clarify your understanding on how the network forward processing works. o1 = torch.mm(net[0].weight,x.t()) + net[0].bias.view(2,1); o1 = torch.nn.Sigmoid().forward(o1).t(); o2 = torch.mm(net[2].weight,o1.t()) + net[2].bias; o2 = torch.nn.Sigmoid().forward(o2); print('Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) :\n',o2) ==> Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) : tensor([[0.5124]], grad_fn=<SigmoidBackward>) For practice, let's try with another examples of input vector. x = torch.tensor([[0.1,0.5]]) print("input = x :\n ",x) ==> input = x : tensor([[0.1000, 0.5000]])
print('net.forward(x) :\n',net.forward(x)) ==> net.forward(x) : tensor([[0.5201]], grad_fn=<SigmoidBackward>)
o1 = torch.mm(net[0].weight,x.t()) + net[0].bias.view(2,1); o1 = torch.nn.Sigmoid().forward(o1).t(); o2 = torch.mm(net[2].weight,o1.t()) + net[2].bias; o2 = torch.nn.Sigmoid().forward(o2); print('Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) :\n',o2) ==> Sigmoid(w1 x1 + b1) => o1 => Sigmoid(w2 o1 + b2) : tensor([[0.5201]], grad_fn=<SigmoidBackward>) Creating a FeedForwardNetwork : 3 Layer
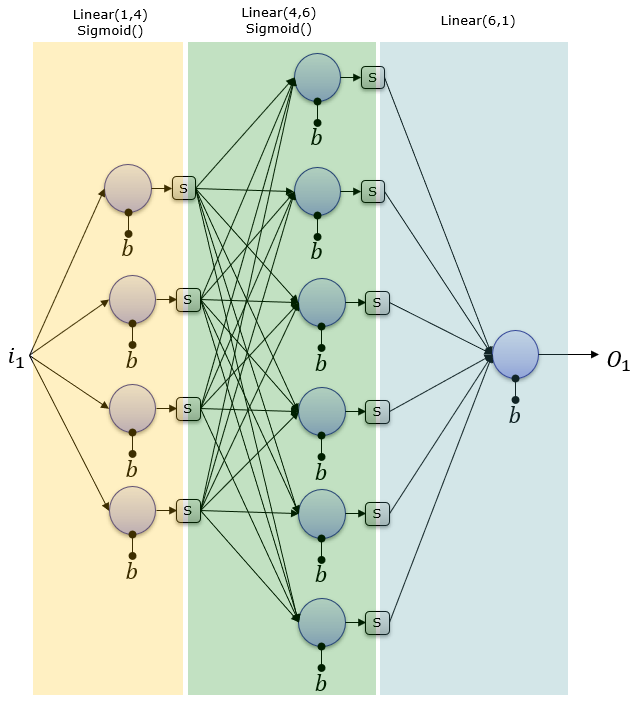
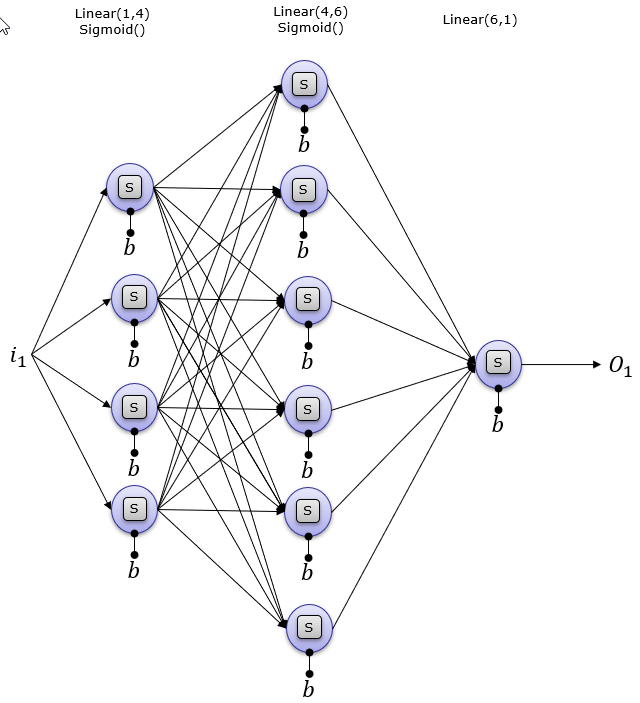
2 Hidden Layers : 4 and 6 Neurons, and 1 Output Neuronsnet = torch.nn.Sequential( torch.nn.Linear(1,4), torch.nn.Sigmoid(), torch.nn.Linear(4,6), torch.nn.Sigmoid(), torch.nn.Linear(6,1) );
print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=1, out_features=4, bias=True) (1): Sigmoid() (2): Linear(in_features=4, out_features=6, bias=True) (3): Sigmoid() (4): Linear(in_features=6, out_features=1, bias=True) )
print('Structure of network net[0] :\n',net[0]) print('Weight of network net[0] :\n',net[0].weight) print('Bias of network net[0] :\n',net[0].bias) ==> Structure of network net[0] : Linear(in_features=1, out_features=4, bias=True) Weight of network net[0] : Parameter containing: tensor([[ 0.2113], [ 0.0598], [-0.5419], [ 0.5640]], requires_grad=True) Bias of network net[0] : Parameter containing: tensor([-0.3503, -0.1059, 0.0805, 0.5176], requires_grad=True)
print('Structure of network net[2] :\n',net[2]) print('Weight of network net[2] :\n',net[2].weight) print('Bias of network net[2] :\n',net[2].bias) ==> Structure of network net[2] : Linear(in_features=4, out_features=6, bias=True) Weight of network net[2] : Parameter containing: tensor([[ 0.3685, 0.3111, -0.1492, -0.0927], [-0.3056, 0.1820, -0.0494, 0.2582], [ 0.1071, -0.2530, 0.4926, -0.0751], [ 0.1456, -0.0216, 0.4323, 0.1524], [-0.4338, 0.1559, 0.0480, -0.2401], [ 0.3520, 0.3001, 0.1065, 0.4229]], requires_grad=True) Bias of network net[2] : Parameter containing: tensor([-0.1031, -0.4883, -0.2630, 0.1407, -0.3158, -0.1010], requires_grad=True)
print('Structure of network net[4] :\n',net[4]) print('Weight of network net[4] :\n',net[4].weight) print('Bias of network net[4] :\n',net[4].bias) ==> Structure of network net[4] : Linear(in_features=6, out_features=1, bias=True) Weight of network net[4] : Parameter containing: tensor([[ 0.3411, -0.3745, -0.0247, 0.0143, 0.2557, -0.3147]], requires_grad=True) Bias of network net[4] : Parameter containing: tensor([-0.2075], requires_grad=True) Backward / Gradient Calculationimport torch
net = torch.nn.Sequential( torch.nn.Linear(2,2), torch.nn.Sigmoid(), torch.nn.Linear(2,1), torch.nn.Sigmoid() ); print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=2, out_features=2, bias=True) (1): Sigmoid() (2): Linear(in_features=2, out_features=1, bias=True) (3): Sigmoid() )
print('Structure of network net[0] :\n',net[0]) print('Weight of network net[0] :\n',net[0].weight) print('Bias of network net[0] :\n',net[0].bias) ==> Structure of network net[0] : Linear(in_features=2, out_features=2, bias=True) Weight of network net[0] : Parameter containing: tensor([[ 0.2781, -0.5925], [ 0.0243, 0.1170]], requires_grad=True) Bias of network net[0] : Parameter containing: tensor([-0.4606, 0.2416], requires_grad=True)
print('Activation function of network net[0]:\n',net[1]) ==> Activation function of network net[0]: Sigmoid()
print('Structure of network net[2] :\n',net[2]) print('Weight of network net[2] :\n',net[2].weight) print('Bias of network net[2] :\n',net[2].bias) ==> Structure of network net[2] : Linear(in_features=2, out_features=1, bias=True) Weight of network net[2] : Parameter containing: tensor([[ 0.6336, -0.5583]], requires_grad=True) Bias of network net[2] : Parameter containing: tensor([0.3790], requires_grad=True)
print('Activation function of network net[2] :\n',net[3]) ==> Activation function of network net[2] : Sigmoid()
print('Weight gradient net[0] \n',net[0].weight.grad) print('Bias gradient net[0] :\n',net[0].bias.grad) print('Weight gradient net[2] \n',net[2].weight.grad) print('Bias gradient net[2] :\n',net[2].bias.grad) ==> Weight gradient net[0] None Bias gradient net[0] : None Weight gradient net[2] None Bias gradient net[2] : None
x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
o = net.forward(x) print('o = net.forward(x) :\n',o) ==> o = net.forward(x) : tensor([[0.5614]], grad_fn=<SigmoidBackward>)
t = torch.tensor([[1.0]]) print('Target :\n',t) ==> Target : tensor([[1.]])
loss = t - o; print('Loss :\n',loss) ==> Loss : tensor([[0.4386]], grad_fn=<SubBackward0>)
loss.backward()
print('Weight gradient net[0] \n',net[0].weight.grad) print('Bias gradient net[0] :\n',net[0].bias.grad) print('Weight gradient net[2] \n',net[2].weight.grad) print('Bias gradient net[2] :\n',net[2].bias.grad) ==> Weight gradient net[0] tensor([[-0.0337, -0.0337], [ 0.0331, 0.0331]]) Bias gradient net[0] : tensor([-0.0337, 0.0331]) Weight gradient net[2] tensor([[-0.0777, -0.1464]]) Bias gradient net[2] : tensor([-0.2462]) Back Propagationimport torch
net = torch.nn.Sequential( torch.nn.Linear(2,2), torch.nn.Sigmoid(), torch.nn.Linear(2,1), torch.nn.Sigmoid() ); print('network structure :\n',net) ==> network structure : Sequential( (0): Linear(in_features=2, out_features=2, bias=True) (1): Sigmoid() (2): Linear(in_features=2, out_features=1, bias=True) (3): Sigmoid() )
print('Structure of network net[0] :\n',net[0]) print('Weight of network net[0] :\n',net[0].weight) print('Bias of network net[0] :\n',net[0].bias) ==> Structure of network net[0] : Linear(in_features=2, out_features=2, bias=True) Weight of network net[0] : Parameter containing: tensor([[-0.1316, -0.3814], [-0.0995, 0.4385]], requires_grad=True) Bias of network net[0] : Parameter containing: tensor([-0.6915, 0.6775], requires_grad=True)
print('Activation function of network net[0]:\n',net[1]) ==> Activation function of network net[0]: Sigmoid()
print('Structure of network net[2] :\n',net[2]) print('Weight of network net[2] :\n',net[2].weight) print('Bias of network net[2] :\n',net[2].bias) ==> Structure of network net[2] : Linear(in_features=2, out_features=1, bias=True) Weight of network net[2] : Parameter containing: tensor([[-0.5374, -0.3386]], requires_grad=True) Bias of network net[2] : Parameter containing: tensor([-0.0594], requires_grad=True)
print('Activation function of network net[2] :\n',net[3]) ==> Activation function of network net[2] : Sigmoid()
print('Weight gradient net[0] \n',net[0].weight.grad) print('Bias gradient net[0] :\n',net[0].bias.grad) print('Weight gradient net[2] \n',net[2].weight.grad) print('Bias gradient net[2] :\n',net[2].bias.grad) ==> Weight gradient net[0] None Bias gradient net[0] : None Weight gradient net[2] None Bias gradient net[2] : None
x = torch.tensor([[1.0,1.0]]) print("input = x :\n ",x) ==> input = x : tensor([[1., 1.]])
o = net.forward(x) print('o = net.forward(x) :\n',o) ==> o = net.forward(x) : tensor([[0.3937]], grad_fn=<SigmoidBackward>)
t = torch.tensor([[1.0]]) print('Target :\n',t) ==> Target : tensor([[1.]])
loss = t - o; print('Loss :\n',loss) ==> Loss : tensor([[0.6063]], grad_fn=<SubBackward0>)
loss.backward()
print('Weight gradient net[0] \n',net[0].weight.grad) print('Bias gradient net[0] :\n',net[0].bias.grad) print('Weight gradient net[2] \n',net[2].weight.grad) print('Bias gradient net[2] :\n',net[2].bias.grad) ==> Weight gradient net[0] tensor([[0.0228, 0.0228], [0.0158, 0.0158]]) Bias gradient net[0] : tensor([0.0228, 0.0158]) Weight gradient net[2] tensor([[-0.0551, -0.1753]]) Bias gradient net[2] : tensor([-0.2387])
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) optimizer.step()
print('New Weight net[0] \n',net[0].weight) print('New Bias gradient net[0] :\n',net[0].bias) print('New Weight net[2] \n',net[2].weight) print('New Bias gradient net[2] :\n',net[2].bias) ==> New Weight net[0] Parameter containing: tensor([[-0.1429, -0.3928], [-0.1074, 0.4306]], requires_grad=True) New Bias gradient net[0] : Parameter containing: tensor([-0.7029, 0.6696], requires_grad=True) New Weight net[2] Parameter containing: tensor([[-0.5099, -0.2509]], requires_grad=True) New Bias gradient net[2] : Parameter containing: tensor([0.0600], requires_grad=True)
|
||