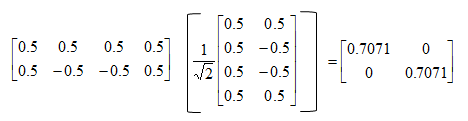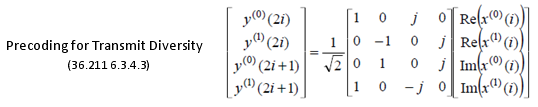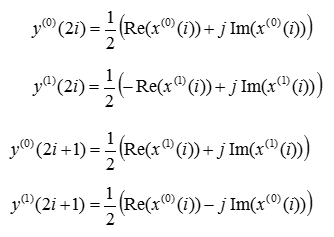Physical Layer Processing is pretty complicated issues. Unlike other layers, it would be very difficult for you to understand the details clearly unless you have very strong academic (theoretical) background. Even when you have pretty strong background in a specific area of PHY layer, some other area of the PHY layer may look completely new to you. It applied to me and I am still in the precess of learning the details piece by piece.

Partly because of the nature of the technology and partly because of my poor organizing skill, this PHY layer process is scattered around multiple different pages and in some case the same topic is described in different pages with a little bit different angle. So sometimes even I have difficulties in finding proper information of PHY process in my own site :).

So I decided to create a kind of 'Contents' (or Index) pages of a book presenting the organization of the book in illustrated format and points the details in the form of hyperlink which are scattered across the whole site.

Every section below draws the same chain for one antenna configuration. User Data goes through Channel Coding and becomes one or two codewords. The Layer Mapper spreads the codewords over layers, Precoding maps the layers to antenna ports, and the Channel Path / Fading block carries the signal to the UE Rx Antenna. So what changes from section to section is mainly the size of each matrix.

Followings are the topics I will talk about in this page.

• Mathematical Background - Matrix, Matrix, Matrix
• 2 x 1 Tx Diversity, 2 Layer, 1 Codeword
• 2 x 2 MIMO, 2 Layer, 2 Codeword
• 4 x 2 MIMO, 2 Layer, 2 Codeword
• 4 x 4 MIMO, 4 Layer, 2 Codeword
• 8 x 2 MIMO, 2 Layer, 2 Codeword
• Reference

Mathematical Background - Matrix, Matrix, Matrix

You don't have to see this section first if you are so allergic to mathematics. I am not making fun of you. I am also allergic to math :). But I strongly recommend you to come back here and see how much this make sense to you. Math itself is not so complicated. The math operation here is the one you might have learned in high school math or in the first or second year in university. As you see, you only have to know how to multiply matrices. The important thing is to understand 'Why we have to this kind of thing in this process ?' and 'what is the physical meaning of each of the matrix and meaning of the operation ?'.  Actually finding/understanding the answers to these questions might be what you would learn in a Ph D course. However, you don't have to be a Ph D.  Don't try to understand this at once and don't get disappointed even when this does not make sense to you when you first look at it. Try to read books, web pages, whitepapers as much as possible and you will gradually catch up the meaning.

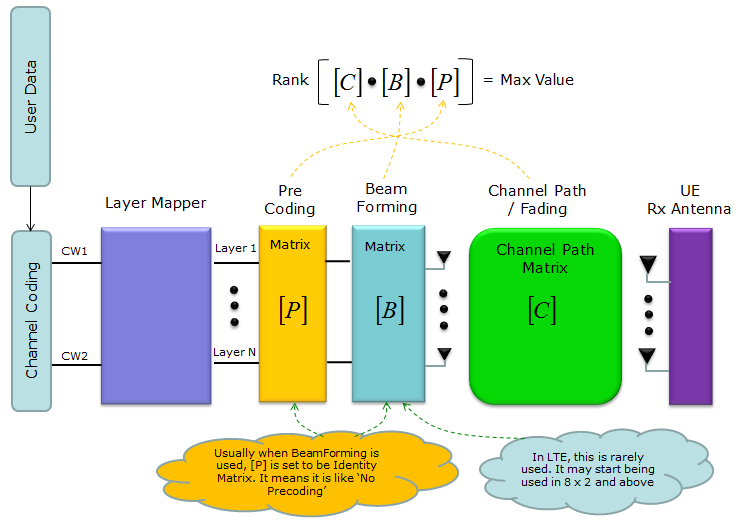
Just as a conclusion, in LTE overall physical layer processing can be illustrated as shown below. The most important thing is to figure out what kind of matrix I have to use for each steps. The simple answer is 'create matrices in such that the rank of matrix product of the whole process become maximum value'.

Here, you would natuarally ask what is 'Rank' ?. Why we need to get max Rank ? For this, you would also need to do some math study. See  Matrix : Rank page. At least, I tried to explain what is Rank and what is the meaning of max rank value.

The whole downlink chain as a product of three matrices. The goal is to keep the rank of [C] [B] [P] at its maximum.

• User Data enters Channel Coding, which produces CW1 and CW2. The Layer Mapper turns them into Layer 1 to Layer N.
• Pre Coding holds the matrix [P], Beam Forming holds [B], and Channel Path / Fading holds the Channel Path Matrix [C]. Dashed arrows tie all three to the formula Rank [C] [B] [P] = Max Value at the top.
• The yellow note says that [P] is usually set to the identity matrix when BeamForming is used, which works like No Precoding.
• The blue note says that [B] is rarely used in LTE, and that it may start being used in 8 x 2 and above.

In real situation, the channel Matrix ([C]) is usually given because it is determined by the channel condition of the communication. We cannot change it as we like. So the only way of getting the max Rank (meaning best MIMO condition) is to change [P] or [B] to make the Rank of the path matrix is as close as possible to the max value. To do this, we need to know of the channel matrix [C]. But transmitter (eNB in LTE downlink case) is not able to know of [C], only receiver can evaluate [C] based on reference signal embedded in the recieved signal. So UE has to figure out what should be the best matrix for [P] or [B] and let transmitter (eNB) know of it. This is the purpose of PMI, RI report.

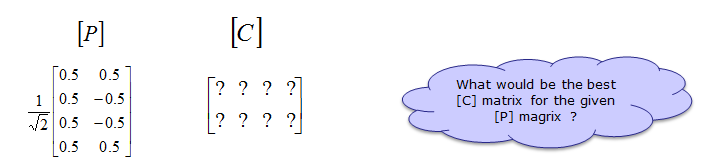
Now let's think of one example of a system using 4 x 2 MIMO. and I assume that Beamforming is not used in this example. In this case, we only have to consider the two matrix [P] and [C].

For this system, we can think of two cases. First we can think of the situation where [C] is given and ask question saying "What is the best [P] matrix for the given [C] matrix ?

The first question: [C] is known and [P] is not.

Next we can think of the situation where [P] is given and ask question saying "What is the best [C] matrix for the given [P] matrix ?

The same question the other way round: [P] is known and [C] is not.

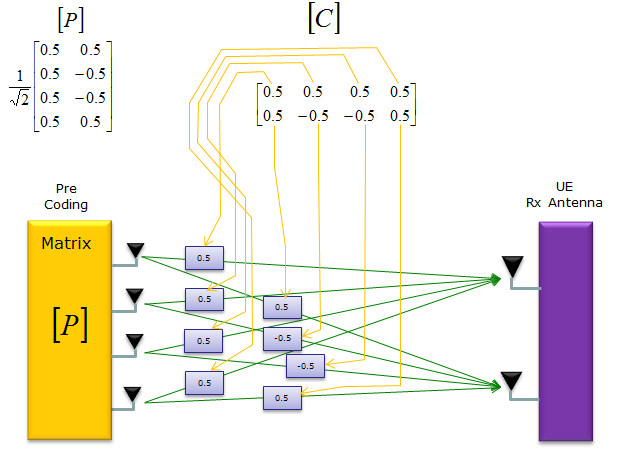
Without going into boring details of mathmatics, let me give you just the answer. If you create [P], [C] as shown below, that can be the best for each other. Of course, if you have different [C], you would need different [P]. (In LTE, various [P] matrix is defined in 3GPP specification and [C] is determined by the communication channel and is estimated (calculated) by UE)

The matched pair drawn as antennas. Each entry of [C] becomes the weight of one path from a Tx antenna to a UE Rx antenna.

• [P] is 1/√2 times a 4 x 2 matrix with columns [0.5 0.5 0.5 0.5] and [0.5 -0.5 -0.5 0.5]. [C] is 2 x 4, with rows [0.5 0.5 0.5 0.5] and [0.5 -0.5 -0.5 0.5].
• The four antennas on the Pre Coding block are the transmit side, and the two antennas on the UE Rx Antenna block are the receive side.
• Eight green paths run from the four Tx antennas to the two Rx antennas. The yellow lines assign each of the eight entries of [C] to one path, so four paths carry 0.5 and the other four carry 0.5, -0.5, -0.5 and 0.5.

You may ask how do I know the [P] and [C] given above is the best combination ?

If you take the product of the two matrix (matrix inner product), you would have following result (If you are familiar with the concept of eigen value/eigen vector or SVD, you would intuitively see the result indicate two independent channel (two non-interfering path)). Also if you take the rank of the resulting matrix, it is 2 (max rank for 2 x 2 matrix). It meets the criteria of the best data path that I explained above.

[C] times [P]. Both off-diagonal entries are 0, so neither layer leaks into the other receive antenna.

The product is easy to check by hand. Row 1 of [C] times column 1 of [P] adds four terms of 0.25, which gives 1, and the factor 1/√2 turns it into 0.7071. Row 1 times column 2 gives 0.25 - 0.25 - 0.25 + 0.25 = 0. The other two entries follow the same way. So the result is a diagonal matrix of rank 2, the maximum for two layers.

This [P] is not an arbitrary choice. It is W₀⁽¹⁴⁾/√2, the two layer entry for codebook index 0 in 36.211 v19.3.0 Table 6.3.4.2.3-2. The generating vector is u₀ = [1 -1 -1 -1]^T, and the superscript (14) takes columns 1 and 4 of W₀. So the example is a real LTE 4 x 2 case. In a real channel, [C] is never this tidy. The UE therefore tests the codebook entries against its channel estimate and reports the best index as PMI, together with the number of layers as RI.

• One goal for the whole chain : the matrix product [C] [B] [P] should keep its maximum rank.
• [C] is given by the channel : only [P] and [B] can be chosen, and only the UE can measure [C].
• A matched [P] makes [C] [P] diagonal : each layer then reaches the UE without interference from the other.
• The example [P] is an LTE codebook entry : W₀⁽¹⁴⁾/√2, index 0 of 36.211 Table 6.3.4.2.3-2.

2 x 1 Tx Diversity, 2 Layer, 1 Codeword

Transmit diversity uses two antennas to make one stream more robust, not to send two streams. The layer mapper still produces two layers from the one codeword, but each layer carries every second symbol. So the data rate is the same as with one antenna, and the gain is diversity.

2 x 1 transmit diversity. One codeword, two layers, and a precoder that is 4 x 4 rather than 2 x 2.

• Channel Coding feeds a single codeword, CW1, into the Layer Mapper, which outputs Layer 1 and Layer 2.
• The Precoding block reads 4 x 4 Diversity Matrix, with a red note to see the Note below for why it is 4 x 4. Two Tx antennas leave the block.
• The Channel Path / Fading block shows a 2 x 1 Matrix for the channel path and a 2 x 2 Matrix for fading. The UE Rx Antenna block has one antenna.
• The label row under the drawing numbers the stages (1) Coding, (2) Layer Mapping, (3) Precoding and (4) Tx/Rx Path/Fading, and the descriptions below follow the same numbers.

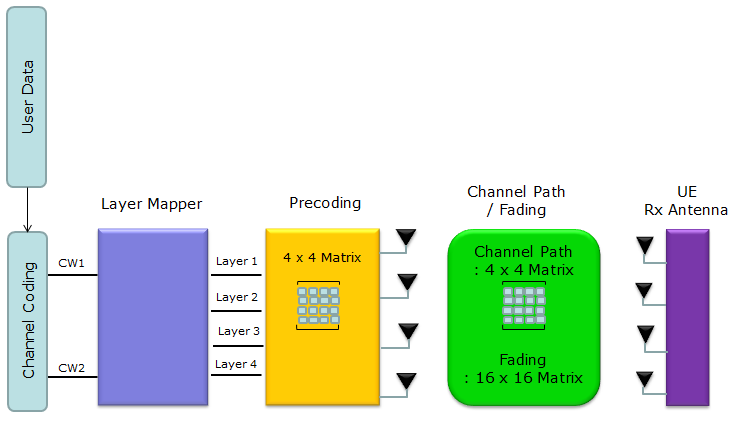
(1) Coding : This is process where user data (bit stream) go through channel coding process and converted to each codeword. DL-SCH coding process as an example, refer to "Channel Coding Processing for DL SCH/PCH/MCH"

(2) Layer Mapping : This is the process where each codeword is mapped to mapped to one or multiple layers. Refer to Layer Mapping page.

(3) Precoding : This is process where the layer data are allocated to multiple antenna ports (logical antenna ports in this stage). See the first section of Precoding page for details.

(4) Channel Path/Fading : you can get the general concept of Channel Path by refering to Channel Modeling page and refer to Fading page to understand how to derive channel correlation matrix.

NOTE :

The reason for 4x4 matrix for 2x1 Tx Diversity is based on following precoding matrix. You may refer to this page if you want to understand fundamental things about Tx Diversity. The conding method in the linked page is not exactly same as this matrix, but you would have some insight on how this precoding works.

The equation below is the one in 36.211 v19.3.0 clause 6.3.4.3. The input vector holds the real and imaginary parts of the two layer symbols x⁽⁰⁾(i) and x⁽¹⁾(i). The output holds two antenna ports at two indices, 2i and 2i+1. That makes four inputs and four outputs, which is the 4 x 4 matrix in the drawing above.

36.211 clause 6.3.4.3. The 4 x 4 matrix acts on real and imaginary parts, which is why a 2 antenna scheme needs a 4 x 4 matrix.

In many cases technical specification represents precoding in matrix form, but sometimes the matrix representation may not be easy for intuitive understanding. I know, for some people those matrix notation may look simpler and more intuitive. If a matrix represenation does not give you any practical understanding, I would suggest you to expend the matrix into ordinary equations as below and think of how the complex and real part of each input data (x()) get distributed into each of the Tx antenna at each transmission timing.

The same precoding written out as four equations. Each antenna sends one layer symbol or the conjugate of the other.

Read the four lines as a pair of pairs. At index 2i, antenna port 0 sends x⁽⁰⁾(i) and port 1 sends -x⁽¹⁾(i)^*. At index 2i+1, port 0 sends x⁽¹⁾(i) and port 1 sends x⁽⁰⁾(i)^*. This is the Alamouti structure. One detail in the drawing needs care. It writes the factor as 1/2, but the matrix in 36.211 carries 1/√2, so each line should start with 1/√2. With 1/√2, the total transmit power stays the same as for one antenna.

The indices 2i and 2i+1 are not two transmission timings in LTE. Resource mapping fills the resource elements in order of frequency first, so the pair usually lands on two adjacent subcarriers of the same OFDM symbol. For this reason LTE transmit diversity is often called SFBC, space frequency block coding.

• Two layers, but one stream of data : each layer carries every second symbol of the one codeword.
• The 4 x 4 matrix works on real and imaginary parts : two ports times two indices gives four outputs.
• The drawing writes 1/2, the spec writes 1/√2 : 36.211 clause 6.3.4.3 uses 1/√2.
• The pair sits in frequency : 2i and 2i+1 usually map to adjacent subcarriers, so the scheme is SFBC.

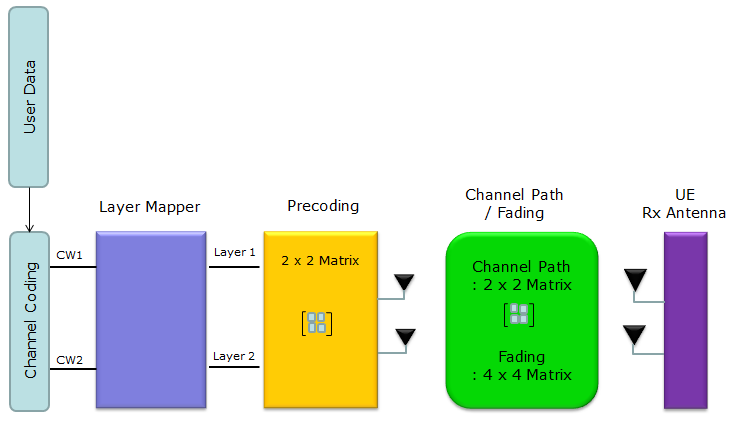
2 x 2 MIMO, 2 Layer, 2 Codeword

With two antennas at the UE as well, the two layers can carry two different codewords. This is spatial multiplexing, and it doubles the peak rate when the channel supports rank 2. It is also the first case where the precoder is a real 2 x 2 matrix chosen from a codebook.

2 x 2 MIMO. Each codeword goes to its own layer, and the precoder is 2 x 2.

• CW1 and CW2 enter the Layer Mapper, and Layer 1 and Layer 2 leave it. With two codewords and two layers, each codeword maps to one layer.
• The Precoding block holds a 2 x 2 Matrix and drives two Tx antennas.
• The Channel Path / Fading block shows a 2 x 2 Matrix for the channel path and a 4 x 4 Matrix for fading. The UE Rx Antenna block has two antennas.

(1) Coding : This is process where user data (bit stream) go through channel coding process and converted to each codeword. DL-SCH coding process as an example, refer to "Channel Coding Processing for DL SCH/PCH/MCH"

(2) Layer Mapping : This is the process where each codeword is mapped to mapped to one or multiple layers. Refer to Layer Mapping page.

(3) Precoding : This is process where the layer data are allocated to multiple antenna ports (logical antenna ports in this stage). See the first section of Precoding page for details.

(4) Channel Path/Fading : you can get the general concept of Channel Path by refering to Channel Modeling page and refer to Fading page to understand how to derive channel correlation matrix.

Note : Since this is one of the simplest form of MIMO (the first steps of MIMO concept), I recommend you to go through MIMO page as well.

For two antenna ports, the codebook is 36.211 v19.3.0 Table 6.3.4.2.3-1. Its two layer column holds only three matrices. Index 0 is the identity divided by √2, and the Precoding page shows that TM3 with large delay CDD uses it. Indices 1 and 2 are 1/2 [1 1; 1 -1] and 1/2 [1 1; j -j], and closed loop TM4 chooses between them from the PMI.

The fading matrix is 4 x 4, not 2 x 2, for a reason worth knowing. It is the spatial correlation matrix of the channel, not the channel itself. 36.101 v20.0.0 Annex B.2.3 builds it as the Kronecker product of the eNodeB correlation matrix and the UE correlation matrix, and 2 x 2 gives a 4 x 4 result. The same rule gives 2 x 2 for the 2 x 1 case above, 8 x 8 for 4 x 2, and 16 x 16 for 4 x 4.

• Two codewords, two layers : each codeword maps to one layer.
• Three 2 layer precoders exist : index 0 for TM3 large delay CDD, indices 1 and 2 for TM4.
• The fading matrix is a correlation matrix : its size is the square of the Tx x Rx antenna count, from 36.101 Annex B.2.3.

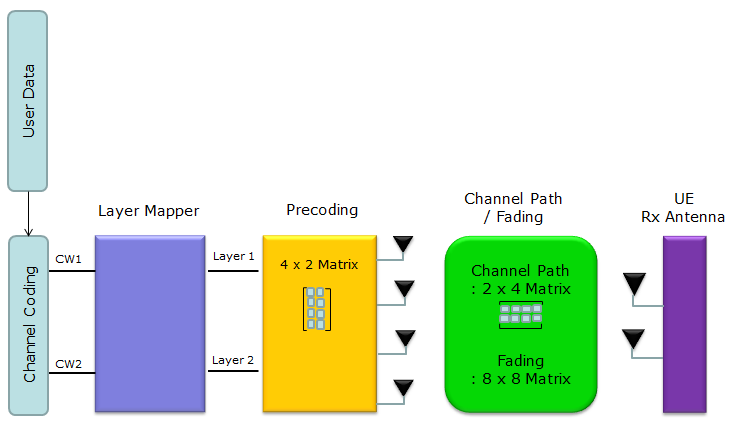
4 x 2 MIMO, 2 Layer, 2 Codeword

Adding two more transmit antennas does not add layers here, because the UE still has only two receive antennas. The rank stays at 2 or less. So the extra antennas are used to shape the two layers, through a 4 x 2 precoder.

4 x 2 MIMO. Two layers spread over four Tx antennas by a 4 x 2 precoder.

• CW1 and CW2 enter the Layer Mapper, and Layer 1 and Layer 2 leave it, as in the 2 x 2 case.
• The Precoding block holds a 4 x 2 Matrix and drives four Tx antennas.
• The Channel Path / Fading block shows a 2 x 4 Matrix for the channel path and an 8 x 8 Matrix for fading. The UE Rx Antenna block has two antennas.

(1) Coding : This is process where user data (bit stream) go through channel coding process and converted to each codeword. DL-SCH coding process as an example, refer to "Channel Coding Processing for DL SCH/PCH/MCH"

(2) Layer Mapping : This is the process where each codeword is mapped to mapped to one or multiple layers. Refer to Layer Mapping page.

(3) Precoding : This is process where the layer data are allocated to multiple antenna ports (logical antenna ports in this stage). The specific Codebook for this configuration is in 4 x 2 MIMO Antenna section (If you are interested in how this codebook is derived, read the whole section of Codebook selection for Precoding - 4 Antenna Ports )

(4) Channel Path/Fading : you can get the general concept of Channel Path by refering to Channel Modeling page and refer to Fading page to understand how to derive channel correlation matrix.

Note : Since this is one of the simplest form of MIMO (the first steps of MIMO concept), I recommend you to go through MIMO page as well.

This configuration is exactly the one in the Mathematical Background section. The 4 x 2 precoder comes from the two layer column of 36.211 Table 6.3.4.2.3-2, which lists 16 entries, and each is divided by √2. The worked example used index 0, W₀⁽¹⁴⁾/√2. The channel matrix is 2 x 4, one row per receive antenna, so [C] [P] is 2 x 2. Its rank can never exceed 2, which is the limit the UE antenna count sets.

• The UE antennas limit the rank : four Tx and two Rx antennas give at most two layers.
• The precoder is 4 x 2 : 16 two layer entries in 36.211 Table 6.3.4.2.3-2, each divided by √2.
• The worked example is this case : W₀⁽¹⁴⁾/√2 is codebook index 0.

4 x 4 MIMO, 4 Layer, 2 Codeword

Four antennas at both ends allow up to four layers. LTE still uses at most two codewords, so the layer mapper now does real work. Each codeword is split over two layers, and the precoder becomes a 4 x 4 matrix.

4 x 4 MIMO. Two codewords over four layers, and every matrix grows to 4 x 4 or larger.

• CW1 and CW2 enter the Layer Mapper, and Layer 1 to Layer 4 leave it.
• The Precoding block holds a 4 x 4 Matrix and drives four Tx antennas.
• The Channel Path / Fading block shows a 4 x 4 Matrix for the channel path and a 16 x 16 Matrix for fading. The UE Rx Antenna block has four antennas.

The layer mapping follows 36.211 v19.3.0 Table 6.3.3.2-1. For four layers and two codewords, x⁽⁰⁾(i) = d⁽⁰⁾(2i) and x⁽¹⁾(i) = d⁽⁰⁾(2i+1) take the first codeword. Then x⁽²⁾(i) = d⁽¹⁾(2i) and x⁽³⁾(i) = d⁽¹⁾(2i+1) take the second. So each codeword feeds two layers, and one transport block with one CRC covers both of them.

The precoder comes from the four layer column of 36.211 Table 6.3.4.2.3-2. There each entry is the full W_n, with its columns in a given order, divided by 2. The fading matrix is 16 x 16, the Kronecker product of two 4 x 4 correlation matrices in 36.101 Annex B.2.3. In a real network rank 4 needs a rich scattering channel with low antenna correlation, so the UE often reports a lower RI, and the eNB sends fewer layers.

The stage descriptions (1) to (4) are the same as in the 4 x 2 section above, and the same Layer Mapping and Precoding pages apply.

• Four layers, still two codewords : each codeword is split over two layers by Table 6.3.3.2-1.
• The precoder is W_n/2 : the four layer column of 36.211 Table 6.3.4.2.3-2.
• Rank 4 depends on the channel : a correlated channel makes the UE report a lower RI.

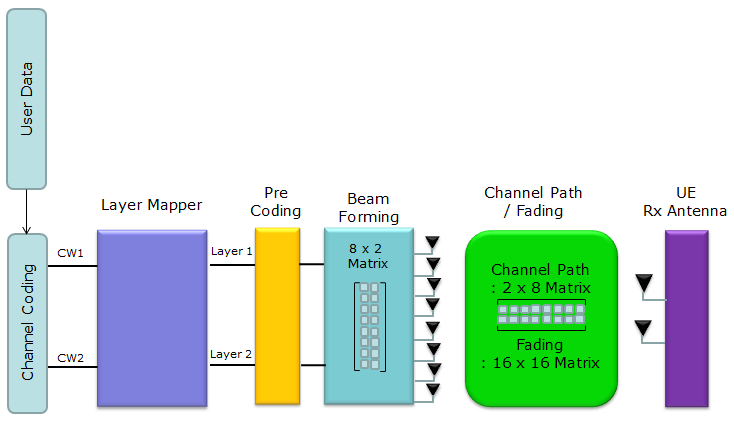
8 x 2 MIMO, 2 Layer, 2 Codeword

Eight transmit antennas change where the matrix sits. The precoding block no longer applies a codebook matrix. Instead, a beamforming block maps two antenna ports onto eight physical antennas, and the UE sees only the two ports.

8 x 2 with beamforming. The 8 x 2 matrix sits in the Beam Forming block, after Pre Coding.

• CW1 and CW2 enter the Layer Mapper, and Layer 1 and Layer 2 leave it.
• The Pre Coding block carries no matrix label. The Beam Forming block holds the 8 x 2 Matrix and drives eight Tx antennas.
• The Channel Path / Fading block shows a 2 x 8 Matrix for the channel path and a 16 x 16 Matrix for fading. The UE Rx Antenna block has two antennas.

(1) Coding : This is process where user data (bit stream) go through channel coding process and converted to each codeword. DL-SCH coding process as an example, refer to "Channel Coding Processing for DL SCH/PCH/MCH"

(2) Layer Mapping : This is the process where each codeword is mapped to mapped to one or multiple layers. Refer to Layer Mapping page.

(3) Precoding : This is process where the layer data are allocated to multiple antenna ports (logical antenna ports in this stage). As of now, 8 x 2 is used only with TM9 (BeamForming). In this case, the procoding is done as described in Precoding for BeamForming . If you see the Precoding process, you would notice the process simply maps each layer to each antenna port(virtual port/UE specific antenna port). No matrix operation is performed in this process.

(4) In 8 x 2, TM 9 case. The matrix operation to map the two virtual antenna port to 8 physical happens in BeamForming process. Here 8 x 2 matrix is applied to the incoming two data stream to map the two stream onto 8 physical antenna. What is the contents of the 8 x 2 matrix ? 3GPP does not specify the contents of the matrix, it simply says "you can use randomly selected matrix". Therefore, in case of 8 x 2, TM9 case, Codebook is not used.. but in some equipment (probably in some live network as well) the codebook specified in 36.213 Table 7.2.4-2 can be used as the beamforming matrix.

If you want to have some CSI report from UE, you can combine CSI specific reference signal as illustrated in Mapping between Antenna port and physical antenna  

(5) Channel Path/Fading : you can get the general concept of Channel Path by refering to Channel Modeling page and refer to Fading page to understand how to derive channel correlation matrix.

Note : Since this is one of the simplest form of MIMO (the first steps of MIMO concept), I recommend you to go through MIMO page as well.

The reason the UE never needs the beamforming matrix is the DM-RS. 36.211 v19.3.0 clause 6.3.4.4 maps the layers to antenna ports 7 and 8, and the UE-specific reference signals on those ports go through the same beamforming as the data. So the UE estimates the effective 2 x 2 channel, beamforming included, and demodulates without knowing the 8 x 2 matrix. The CSI-RS on ports 15 to 22 serve a different purpose. They let the UE measure the eight antenna channel and report CSI, for example with the two layer codebook of 36.213 v19.4.0 Table 7.2.4-2.

• The 8 x 2 matrix belongs to beamforming : precoding only maps the two layers to ports 7 and 8.
• The UE demodulates from DM-RS : the DM-RS is beamformed like the data, so the matrix stays transparent.
• CSI-RS is for feedback : ports 15 to 22 let the UE report CSI on the eight antenna channel.

Reference

• 3GPP TS 36.211 v19.3.0 - clause 6.3.3.2 layer mapping for spatial multiplexing, clause 6.3.4.2.3 codebook for precoding, clause 6.3.4.3 precoding for transmit diversity, clause 6.3.4.4 precoding with UE-specific reference signals
• 3GPP TS 36.101 v20.0.0 - Annex B.2.3, MIMO channel correlation matrices
• 3GPP TS 36.213 v19.4.0 - Table 7.2.4-2, codebook for 2-layer CSI reporting using antenna ports 15 to 22