|
Engineering Math - Calculus |
||
|
Slope and Derivative
If you are already familiar with Calculus, just skip this page. Probably you would easily get bored. But if you fall into any one of the following list, this post would help you.
i) I think I need to study Calculus, but I already got scared of such a big word 'Calculus'. I want to start with more easy and familiar terms. ii) It's been a long time since I complete my school math (high school, early colledge), I want to fresh up my memory. iii) I have kids or sister/brothers who just about to study calculus and I want to give them some 'Pre-Calculus' tips.
Simply put, 'Calculus' is to study on 'Rate of Change'. As in any other topics, the best way to understand this concept is to start with something visual. As you know, the most common visual thing in math is 'Graph'. So I will start with several graphs to explain the concept of 'Rate of Change' and how it will lead to the concept of calculus.
The rate of change in a graph is represented as 'Slope'. What does it mean by 'Slope' ? Actually you don't need to be a math geek to understand the concept of Slope. Everybody already knows what the Slope means.
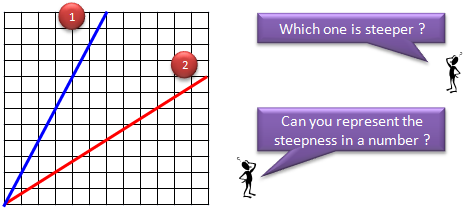
I have two lines in a graph as shown below. If I ask 'Which of the lines is steeper ?', everybody would come out with answer right away. Line (1) is steeper. Then what if I ask 'How do you represent the steepness in a number ?'. Then you may start scratching your head.
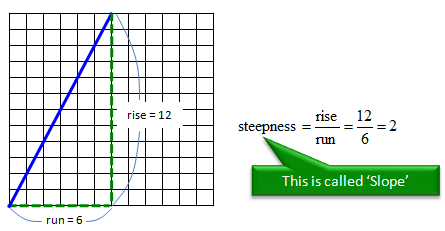
Now let's think about the second question, which is "'How do you represent the steepness in a number ?" Steepness is defined as follows. It is just a ratio of 'run' and 'rise'. 'Run' indicate the changes in the horizontal direction and 'Rise' indicate the changes in the vertical direction.
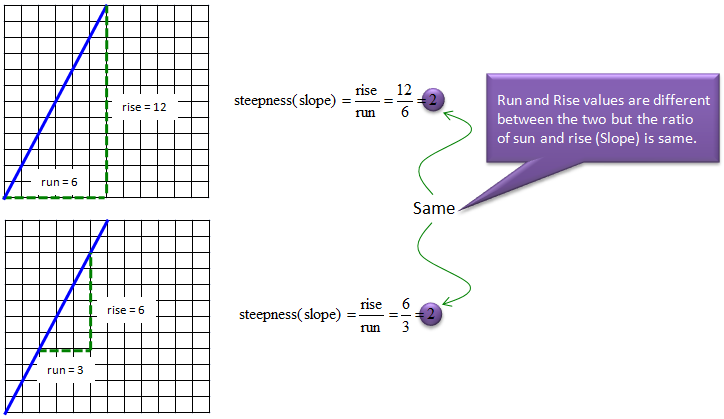
There can be many different ways to define 'run' and 'rise' on a graph. But if the line is 'straight', it doesn't matter how you define the 'run' and 'rise'. As shown in the following example. As long as you define in such a way that 'run' line meets 'rise' line at one point in 90 degree, the ratio of rise and run is always same.
We now know how to represent a steepness into a number. Then what is slope ? Slope is just another name for steepness. They are same thing.
I think most of you can recall that you had dealt with this kind of things while you are in high school physics class. You maight have not noticed that this is related to such a big word 'Calculus', but this would give you the insight of the most important aspect of Calculus and this would help you with even university Calculus course as well.
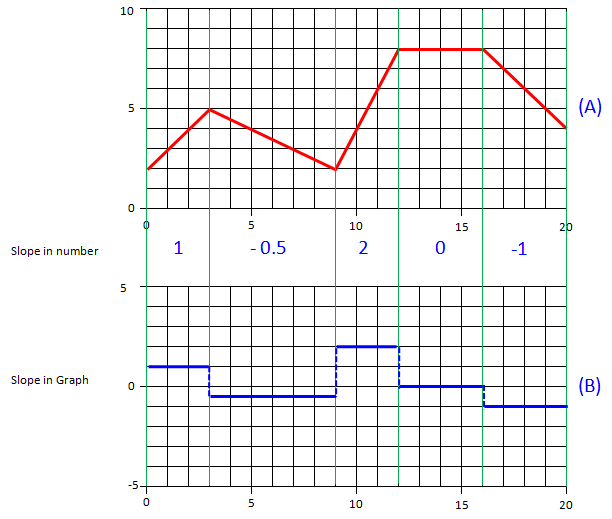
Let's suppose that we have a graph as shown in graph (A). You would not see this kind of graph (made up of multiple segments rather than nice/smooth single curve) in math class, but you would see this kind of graphs pretty often in physics course or more often in various engineering course. In real life, there are not many cases where you can explain with a single/smooth function and in more case you would have to split it into multiple segments and come out with different equations for each of the segments. In this case, you can have the segmented graph as in this example.
Anyway getting back to our main topic (not much about the physical meaning of it), you may intuitively identify the range of each segment of the graph (the green vertical line shows the boundary of each segment). Now I would ask you to figure out the slope of each segment of Graph (A). Just based on what I explained above or from high school math class, you can easily come out with the slope value for each of the segment. If you plot the slope of each segment into a graph, you can get a graph (B). Can you clearly understand the relationship between Graph (A) and Graph (B). In mathematica terms, we can say Graph (B) is the derivative of Graph (A). The process of figuring out Graph (B) from Graph (A) is called 'Differentiation'.
Linking to Real World (Physics)
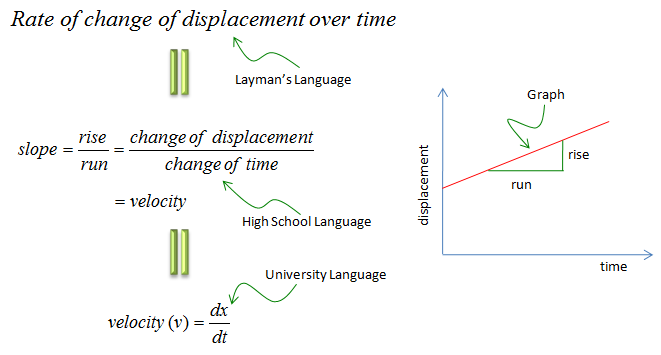
Now let's think of a couple of real life issues and see how it can be associated with the concept of calculus. First look at the graph on the right side, it would be a kind of graph you might have seen in your high school physics. The horizontal axis represents 'time' and vertical axis represents 'displacement'. The red line on the plot represents the relation between time and displacement. What is the meaning of the slope of the graph ? Three different types of answers are shown on the left side. I hope you will get familiar with all of the different ways of representation.
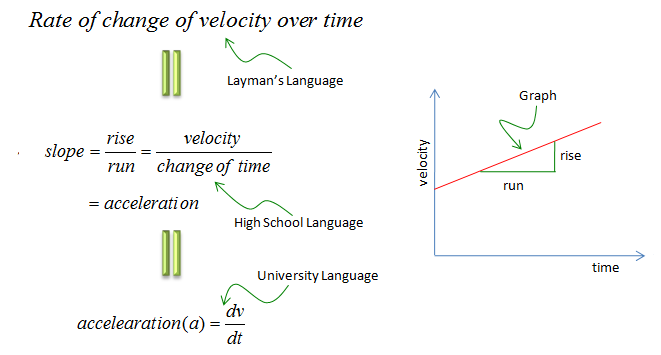
Now look at another example. Look at the graph on the right side, it is exactly the same shape of the graph as you have seen in previous example. The only difference is the meaning of the vertical axis. The horizontal axis represents 'time' and vertical axis represents 'velocity'. The red line on the plot represents the relation between time and velocity. What is the meaning of the slope of the graph ? Three different types of answers are shown on the left side. I hope you will get familiar with all of the different ways of representation.
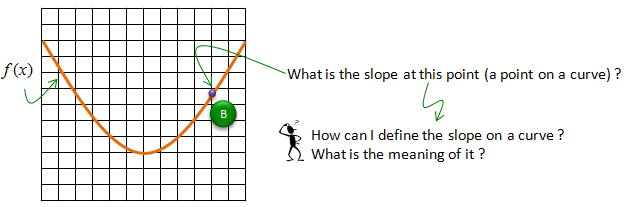
Now let's think of a little bit tricky situation. Suppose you are told to figure out the slope at a point on a curve as shown below.
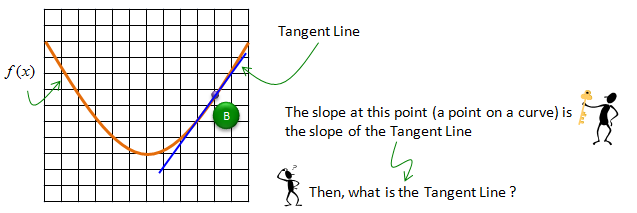
Assuming that you haven't got any basic calculus course, your first response would be "I learned only about getting the slope on a straight line. What do you mean by getting the slope on a curve ?". It is a good question. The first step is to figure out the meaning (definition) of the slope on a curve. The slope on a curve is defined as the slope of the straight line which is tangential to the point on the curve as illustrated below.
Now I know what you will ask next -:). You would ask what is Tangent line ? The definition of tagential line goes as follows.
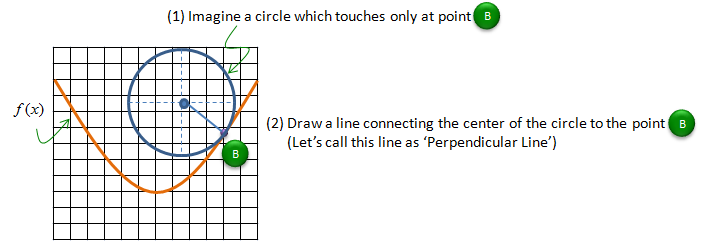
First, think that you have an imaginary circle which is touches on only one point (point B as shown below). Then draw a line between the center of the circle and the point (Point B) on the curve.
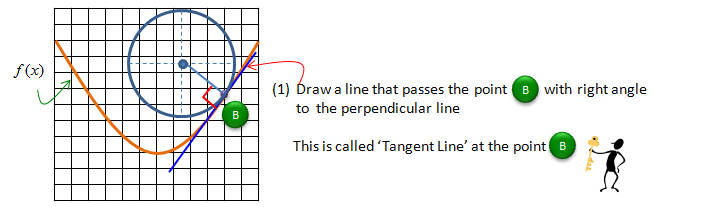
Now draw a line which is passing through the point and form the right angle to the line you draw above. This line is called the tangential line of the curve on a point (B).
Now with a long procedure, we figured out how to get the tangential line of a curve at a certain point. When you are told to get a slope on a curve at a certain point, what you have to do is to get a slope of the tagent line on a curve at the specified point.
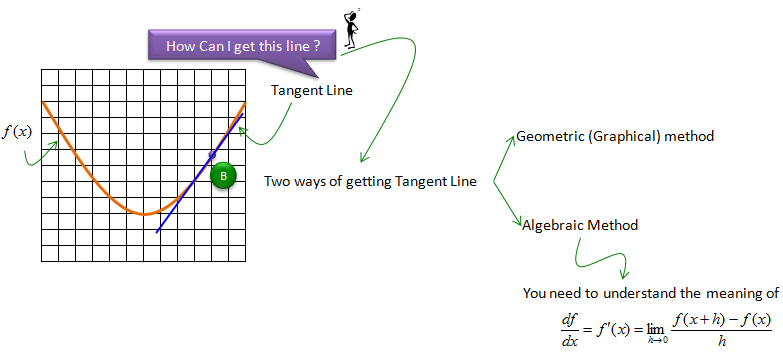
Then how can I calculate the slope of the tangent line ? Do I have to go through the long procedure explained above every time ?. Fortunately you have a better way as summarized below. There are mainly two method. One is a kind of Geometrical/Graphical method and the other method is Algebraic method.
Actually the algebraic method shown above is the center piece of 'Calculus' which will be explained in detail in the concept of Limit page.
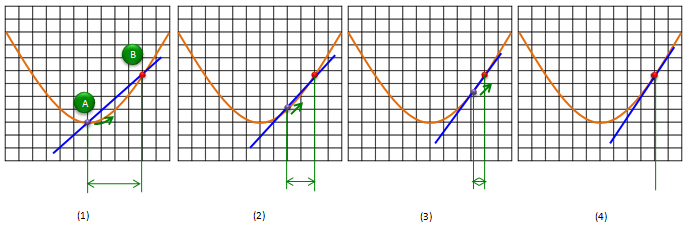
Here in this page, let's briefly think of the graphical method. (Even though I said 'Graphical Method', it still need a little bit of basic calculation'. That calculation is same as what you have done to get the slope of straight line at the beginning of this page). Before I explain the procedure, I would like you to go through the following sequence of graphs and see if you figure out the method on your own. Start from graph (1) and move to (2) and (3) and (4). The last graph (Graph (4)) would give you the slope of the tagential line.
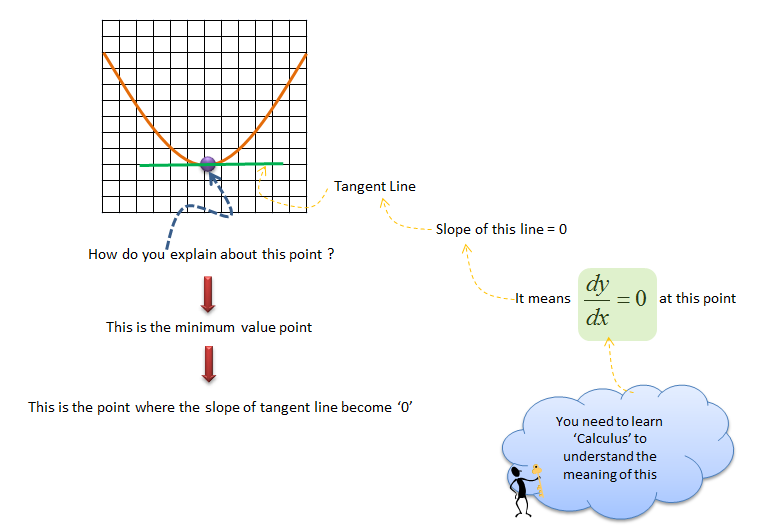
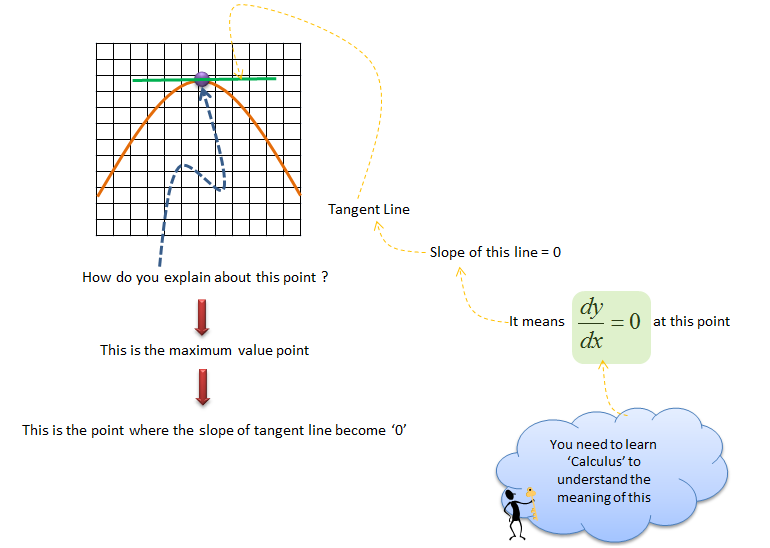
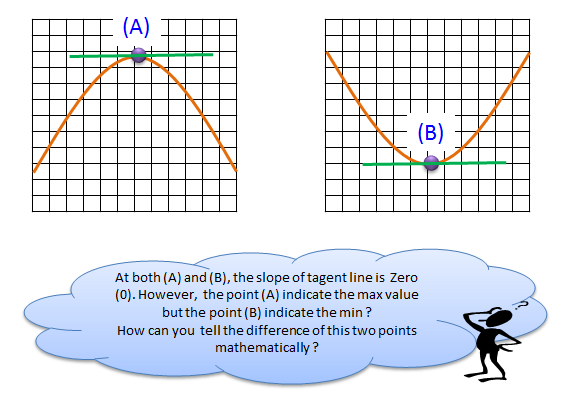
Application of a Tangent Line - Finding Min/Max
How to Solve a problem ?
Derivative Table : Click Here Differentiation Rule : Click Here
|
||