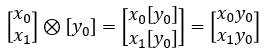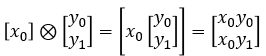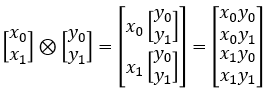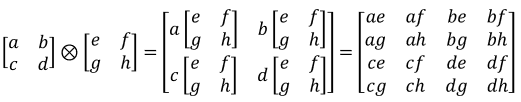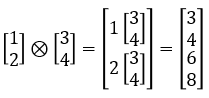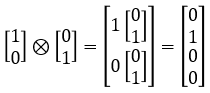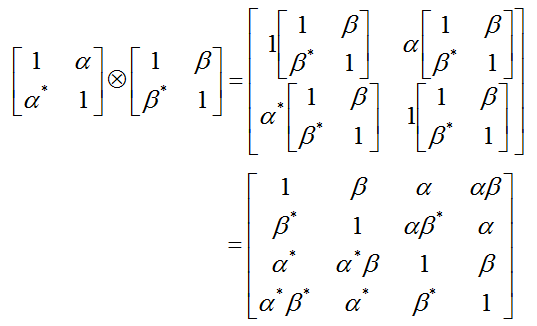|
Engineering Math - Matrix |
||
|
Tensor Product/Kronecker product
Tensor Product / Kronecker product is a way of creating a vector space from other vectors (like dot produt, cross product). The operation is defined as follows. It is hard for me to explain on mathematical meaning of Tensor product and I would focus more on the application of Tensor product. For the detailed explanation with mathematical point of view, refer to Ref [1].
Some Intuition
When I first saw this operation and being used very often in my field (wireless communication), I asked myself 'what would be the original motivation that triggered invention of this operator? what this operator really do ? what is the practical meaning of this operation ?'. I searched quite a lot on the web trying to find the answers to these questions but failed to find any clear answers. So even as of now, I don't the answer. However, while I was writing the examples of this operator many times, an intuition struck myself. My intuition goes like this. If I express a vector or matrix in a set, this operator gives all the possible mapping between the elements of the sets, meaning giving all the possible combinations of the elements of the sets.
Let me illustrate some examples based on this intuition.
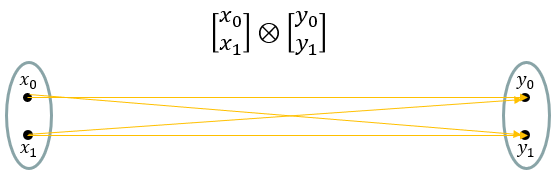
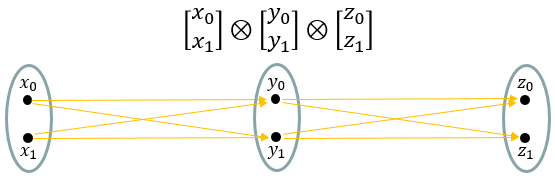
Let's suppose we have two vectors and represents the two vectors into sets as shown below.
Then the kreonecker product of the two vectors can be represented as all the possible mapping between the two vectors as represented by arrows shown below.
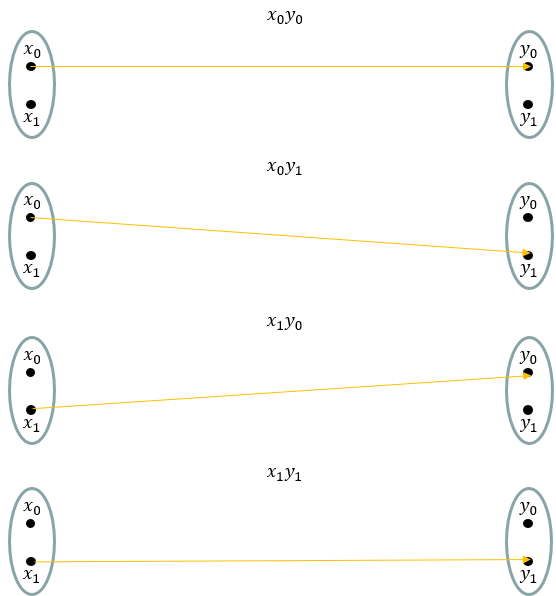
Each elements in the result of the kronector product corresponds to each cases of mapping as illstrated below.
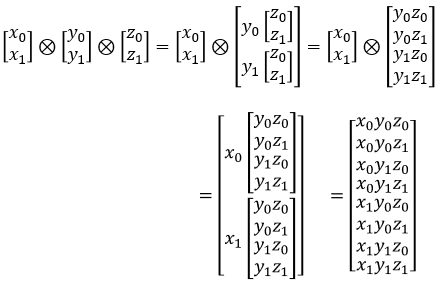
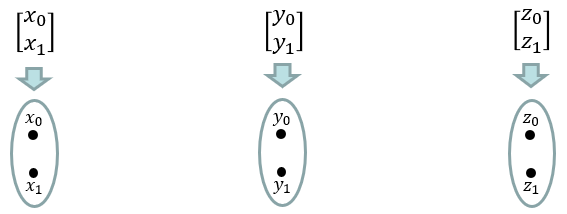
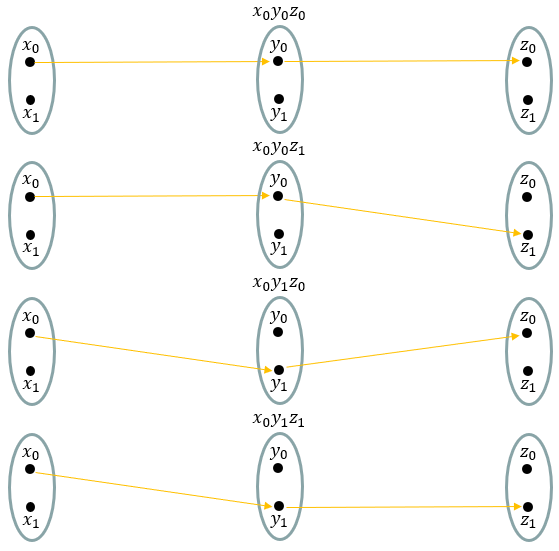
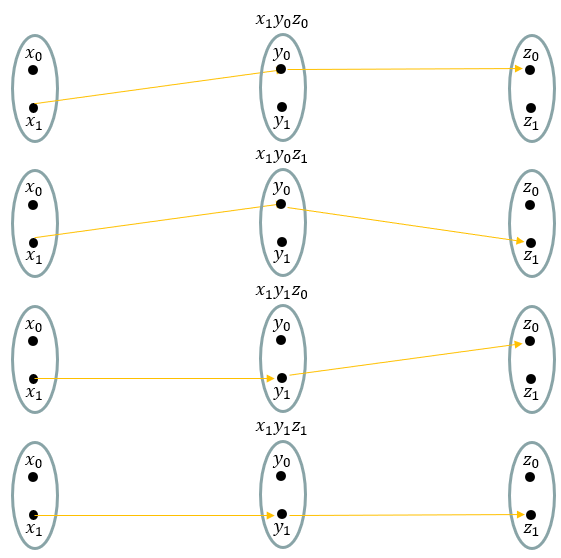
Now let's consider the case where three vectors are involved. Consider a case where we have three vectors that is represented in sets as shown below.
The kronecker product of these three vectors can be represented as a mapping among the three vectors as shown below.
Each elements in the resulting matrix of the kronecker product of the three vectors can be illustrated as each mapping among the three sets as shown below.
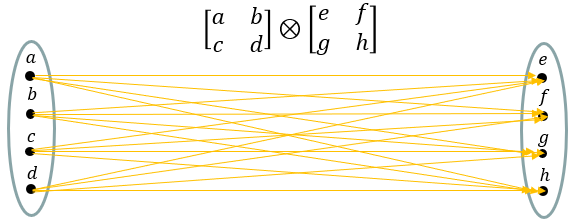
Now let's think of a cases where two matrices (not vector) are used. Consider we have two matrices that are represented as sets as shown below. Here, I just flatten out the matrix into a set. This mean that I lose the structural information of the matrix (i.e, lose the information of colums, rows). This would imply that my intuition is not correct in terms of strict mathematical definition, but I think it still be useful to understand the basic nature of the operation.
Still by the same logic as above, the kronecker product of the two matrix can be represented as all the possible mapping between the elements of each matrices as shown below. Again, this mapping would now show the structural information (i.e, column and row position) of the operation, but it still gives you all the elements in the resulting matrix of the operation.
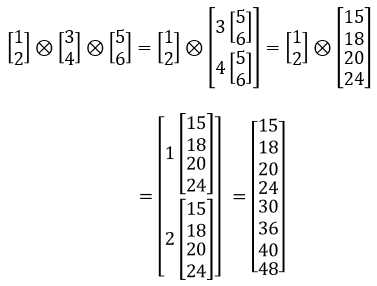
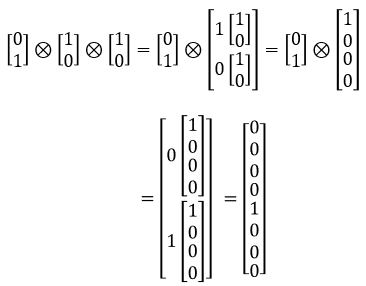
Examples
Example 1 >
Example 2 >
Example 3 > This is the way by which we can represent multiple quantum bits into a vector. (See this page for the details of Quantum bit(Q bit) representation).
Example 4> Derivation of Hamadard Matrix. This is a method that are commonly used to generate othogonal code sequence in communication system. Walsh Code is an example of this.
See Hamadard Matrix page
Example 5> Antenna Correlation Matrix in MIMO Fading
Following is an exmple of applying Tensor Product Operation. This shows how MIMO correlation matrix between UE and eNB can be derived from UE and gNB antenna correlation coefficient.
Reference
[1] The Tensor Product, Demystified
|
||