Python

  

 

 

 

PyTorch - nn.Linear

 

 

nn.Linear(n,m) is a module that creates single layer feed forward network with n inputs and m output. Mathematically, this module is designed to calculate the linear equation Ax = b where x is input, b is output, A is weight. This is where the name 'Linear' came from.

 

 

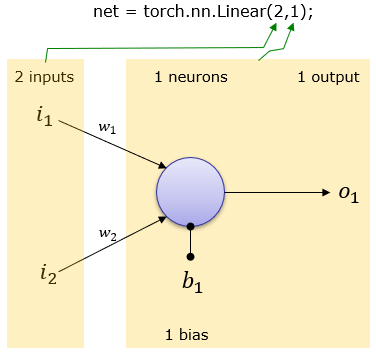
NOTE : The Pytorch version that I am using for this tutorial is as follows.

    >>> print(torch.__version__)

          1.0.1

 

 

 

Creating a FeedForwardNetwork

 

To use nn.Linear module, you have to import torch as below.

    import torch

 

 

 

2 Inputs and 1 output (1 neuron)

 

    net = torch.nn.Linear(2,1);

     

    This creates a network as shown below. Weight and Bias is set automatically.

     

     

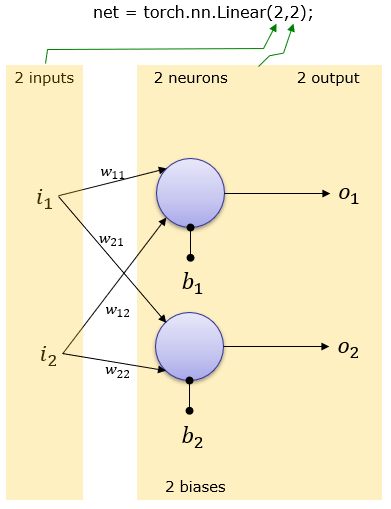
    You can print out overal network structure and Weight & Bias that was automatically set as follows.

     

    print('network structure : torch.nn.Linear(2,1) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(2,1) :

                        Linear(in_features=2, out_features=1, bias=True)

           Weight of network :

                        Parameter containing:

                                 tensor([[ 0.6930, -0.2363]], requires_grad=True)

           Bias of network :

                        Parameter containing:

                                 tensor([0.3855], requires_grad=True)

 

 

 

2 Inputs and 2 outputs (2 neuron)

 

    net = torch.nn.Linear(2,2);

     

    This creates a network as shown below. Weight and Bias is set automatically.

     

     

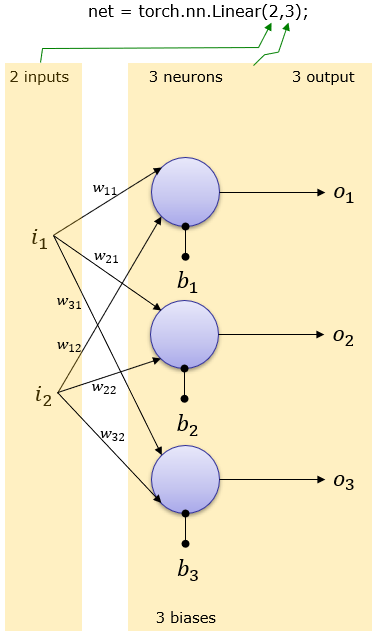
    You can print out overal network structure and Weight & Bias that was automatically set as follows.

    print('network structure : torch.nn.Linear(2,2) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(2,2) :

                        Linear(in_features=2, out_features=2, bias=True)

          Weight of network :

                        Parameter containing:

                                  tensor([[ 0.4992, -0.1154],

                                             [ 0.2762, -0.0332]], requires_grad=True)

           Bias of network :

                        Parameter containing:

                                  tensor([-0.5019,  0.2884], requires_grad=True)

 

 

 

2 Inputs and 3 output (3 neuron)

 

    net = torch.nn.Linear(2,3);

     

    This creates a network as shown below. Weight and Bias is set automatically.

     

     

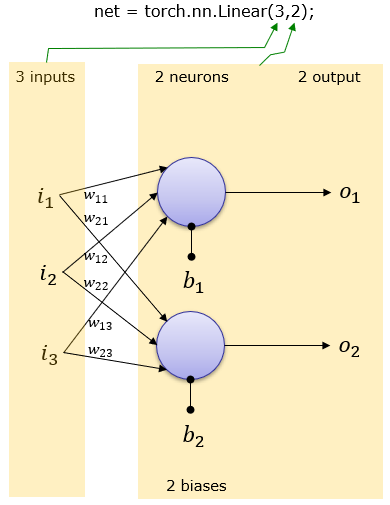
    You can print out overal network structure and Weight & Bias that was automatically set as follows.

    print('network structure : torch.nn.Linear(2,3) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(2,3) :

                        Linear(in_features=2, out_features=3, bias=True)

          Weight of network :

                        Parameter containing:

                                 tensor([[ 0.2799,  0.6430],

                                            [ 0.4635, -0.2675],

                                            [-0.1784, -0.4651]], requires_grad=True)

          Bias of network :

                        Parameter containing:

                                 tensor([-0.3769, -0.2818, -0.4946], requires_grad=True)

 

 

 

3 Inputs and 2 output (2 neuron)

 

    net = torch.nn.Linear(3,2);

     

    This creates a network as shown below. Weight and Bias is set automatically.

     

     

    You can print out overal network structure and Weight & Bias that was automatically set as follows.

    print('network structure : torch.nn.Linear(3,2) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(3,2) :

                        Linear(in_features=3, out_features=2, bias=True)

          Weight of network :

                        Parameter containing:

                                  tensor([[ 0.3149, -0.0778,  0.0579],

                                             [ 0.0947,  0.0997,  0.2743]], requires_grad=True)

                        Bias of network :

                                  Parameter containing:

                                            tensor([-0.4785, -0.1434], requires_grad=True)

 

 

 

FeedForward Evaluation

 

 

2 Inputs and 1 output (1 neuron)

     

    net = torch.nn.Linear(2,1);

    print('network structure : torch.nn.Linear(2,1) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

     

    This create a network with 2 inputs and 1 output,  and print out informations about the network as follows.

    ==> network structure : torch.nn.Linear(2,1) :

                        Linear(in_features=2, out_features=1, bias=True)

          Weight of network :

                       Parameter containing:

                                tensor([[0.0634, 0.3101]], requires_grad=True)

          Bias of network :

                      Parameter containing:

                               tensor([0.0953], requires_grad=True)

     

     

    Now creates an input vector as you like.

     

    x = torch.tensor([[1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                     tensor([[1., 1.]])

     

    You can evalute the network with the input vector that you have specified using forward() function as shown below (perform the linear formula Ax where A is weight matrix, x is input vector).

     

    print('net.forward(x) :\n',net.forward(x))

    ==> net.forward(x) :

                    tensor([[0.4688]], grad_fn=<AddmmBackward>)

     

    You can verify the evaluation result by doing the Ax on your own without using forward() function as follows. This shows the same result as the one you got with forward() function.

     

    o = torch.mm(net.weight,x.t()) + net.bias;

    print('w x + b :\n',o)

    ==> w x + b :

                    tensor([[0.4688]], grad_fn=<AddBackward0>)

     

     

    For practice, let's try with another input vector as below.

     

    x = torch.tensor([[0.1,0.5]])

    print("input = x :\n ",x)

    print('net.forward(x) :\n',net.forward(x))

    o = torch.mm(net.weight,x.t()) + net.bias;

    print('w x + b :\n',o)

    print("\n")

    ==>

         input = x :

                   tensor([[0.1000, 0.5000]])

         net.forward(x) :

                   tensor([[0.2567]], grad_fn=<AddmmBackward>)

         w x + b :

                  tensor([[0.2567]], grad_fn=<AddBackward0>)

 

 

 

2 Inputs and 2 output (2 neuron)

 

    net = torch.nn.Linear(2,2);

    print('n2etwork structure : torch.nn.Linear(2,2) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

     

    This create a network with 2 inputs and 2 output,  and print out informations about the network as follows.

    ==> network structure : torch.nn.Linear(2,2) :

                       Linear(in_features=2, out_features=2, bias=True)

          Weight of network :

                       Parameter containing:

                                tensor([[ 0.1765, -0.5866],

                                          [-0.1639, -0.6669]], requires_grad=True)

         Bias of network :

                     Parameter containing:

                               tensor([-0.0817,  0.5753], requires_grad=True)

     

     

    Now creates an input vector as you like.

     

    x = torch.tensor([[1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                     tensor([[1., 1.]])

     

    You can evalute the network with the input vector that you have specified using forward() function as shown below (perform the linear formula Ax where A is weight matrix, x is input vector).

     

    print('net.forward(x) :\n',net.forward(x))

    ==> net.forward(x) :

                   tensor([[-0.4917, -0.2555]], grad_fn=<AddmmBackward>)

     

    You can verify the evaluation result by doing the Ax on your own without using forward() function as follows. This shows the same result as the one you got with forward() function.

     

    o = torch.mm(net.weight,x.t()) + net.bias.view(2,1);

    print('w x + b :\n',o)

    ==> w x + b :

                   tensor([[-0.4917],

                             [-0.2555]], grad_fn=<AddBackward0>)

     

     

    For practice, let's try with another input vector as below. (NOTE : I changed the shape of bias vector. Try this without changing the shape of the bias vector and how the result get different).

     

    x = torch.tensor([[0.1,0.5]])

    print("input = x :\n ",x)

    print('net.forward(x) :\n',net.forward(x))

    o = torch.mm(net.weight,x.t()) + net.bias.view(2,1);

    print('w x + b :\n',o)

    print("\n")

    ==>

        input = x :

                  tensor([[0.1000, 0.5000]])

        net.forward(x) :

                  tensor([[-0.3573,  0.2255]], grad_fn=<AddmmBackward>)

        w x + b :

                  tensor([[-0.3573],

                             [ 0.2255]], grad_fn=<AddBackward0>)

 

 

 

2 Inputs and 3 output (3 neuron)

 

 

    net = torch.nn.Linear(2,3);

    print('network structure : torch.nn.Linear(2,3) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

     

    This create a network with 2 inputs and 3 output,  and print out informations about the network as follows.

    ==> network structure : torch.nn.Linear(2,3) :

                               Linear(in_features=2, out_features=3, bias=True)

          Weight of network :

                              Parameter containing:

                                       tensor([[ 0.5580,  0.1612],

                                                  [-0.4506,  0.2371],

                                                  [-0.5267, -0.1745]], requires_grad=True)

         Bias of network :

                            Parameter containing:

                                      tensor([-0.2699, -0.6810,  0.3995], requires_grad=True)

     

     

    Now creates an input vector as you like.

     

    x = torch.tensor([[1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                     tensor([[1., 1.]])

     

    You can evalute the network with the input vector that you have specified using forward() function as shown below (perform the linear formula Ax where A is weight matrix, x is input vector).

     

    print('net.forward(x) :\n',net.forward(x))

    ==> net.forward(x) :

                   tensor([[ 0.4493, -0.8945, -0.3017]], grad_fn=<AddmmBackward>)

     

    You can verify the evaluation result by doing the Ax on your own without using forward() function as follows. This shows the same result as the one you got with forward() function. (NOTE : I changed the shape of bias vector. Try this without changing the shape of the bias vector and how the result get different).

     

    o = torch.mm(net.weight,x.t()) + net.bias.view(3,1);

    print('w x + b :\n',o)

    ==> w x + b :

                   tensor([[ 0.4493],

                              [-0.8945],

                              [-0.3017]], grad_fn=<AddBackward0>)

     

     

    For practice, let's try with another input vector as below.

     

    x = torch.tensor([[0.1,0.5]])

    print("input = x :\n ",x)

    print('net.forward(x) :\n',net.forward(x))

    o = torch.mm(net.weight,x.t()) + net.bias.view(3,1);

    print('w x + b :\n',o)

    print("\n")

    ==>

        input = x :

                  tensor([[0.1000, 0.5000]])

        net.forward(x) :

                 tensor([[-0.1335, -0.6075,  0.2596]], grad_fn=<AddmmBackward>)

        w x + b :

                 tensor([[-0.1335],

                            [-0.6075],

                            [ 0.2596]], grad_fn=<AddBackward0>)

 

 

 

3 Inputs and 2 output (2 neuron)

 

 

    net = torch.nn.Linear(3,2);

    print('network structure : torch.nn.Linear(3,2) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

     

    This create a network with 3 inputs and 2 output,  and print out informations about the network as follows.

    ==> network structure : torch.nn.Linear(3,2) :

                               Linear(in_features=3, out_features=2, bias=True)

          Weight of network :

                               Parameter containing:

                                         tensor([[-0.5554,  0.0235,  0.5508],

                                                    [-0.1813, -0.4785, -0.4031]], requires_grad=True)

         Bias of network :

                             Parameter containing:

                                       tensor([-0.1049,  0.0320], requires_grad=True)

     

     

    Now creates an input vector as you like.

     

    x = torch.tensor([[1.0,1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                     tensor([[1., 1., 1.]])

     

    You can evalute the network with the input vector that you have specified using forward() function as shown below (perform the linear formula Ax where A is weight matrix, x is input vector).

     

    print('net.forward(x) :\n',net.forward(x))

    ==> net.forward(x) :

                    tensor([[-0.0860, -1.0309]], grad_fn=<AddmmBackward>)

     

    You can verify the evaluation result by doing the Ax on your own without using forward() function as follows. This shows the same result as the one you got with forward() function. (NOTE : I changed the shape of bias vector. Try this without changing the shape of the bias vector and how the result get different).

     

    o = torch.mm(net.weight,x.t()) + net.bias.view(2,1);

    print('w x + b :\n',o)

    ==>w x + b :

                    tensor([[-0.0860],

                               [-1.0309]], grad_fn=<AddBackward0>)

     

     

    For practice, let's try with another input vector as below.

     

    x = torch.tensor([[0.1,0.5,1.0]])

    print("input = x :\n ",x)

    print('net.forward(x) :\n',net.forward(x))

    o = torch.mm(net.weight,x.t()) + net.bias.view(2,1);

    print('w x + b :\n',o)

    ==>

        input = x :

                    tensor([[0.1000, 0.5000, 1.0000]])

        net.forward(x) :

                   tensor([[ 0.4021, -0.6285]], grad_fn=<AddmmBackward>)

        w x + b :

                   tensor([[ 0.4021],

                             [-0.6285]], grad_fn=<AddBackward0>)

 

 

 

Backward / Gradient Calculation

 

The procedures to be implemented in this section can be summarized as follows. The main purpose in this section is to define a complete forward path for a linear network.

 

Step 1

Define a Network

Step 2

Create a sample Input Data

Step 3

Define a procedure to caclulate the Output (this is called 'Foward' procedure)

Step 4

Define the desired output for the input data

Step 5

Calculate the Output data (Estimated Output) using the input and Forward procedure(Step 3)

Step 6

 Calculate the Error from the Estimated Output and Desired Output. This Error is called 'Loss'

Step 7

 Caculate the gradient

 

    import torch

     

Define a simple linear network that has two inputs and one output. This will create a network as shown here. And print out the weight and bias set automatically by Pytorch. Basically, these initial values would be assigned randomly, so every time you run the script you would get different weight and bias values.

    net = torch.nn.Linear(2,1);

    print('network structure : torch.nn.Linear(2,1) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(2,1) :

                   Linear(in_features=2, out_features=1, bias=True)

           Weight of network :

                   Parameter containing:

                          tensor([[0.1333, 0.6570]], requires_grad=True)

           Bias of network :

                   Parameter containing:

                          tensor([-0.2780], requires_grad=True)

 

Now let's check if there is any gradient value set by defaut. As you see here, the gradient value is not set automatically.

    print('Weight gradient \n',net.weight.grad)

    print('Bias gradient :\n',net.bias.grad)

    ==> Weight gradient      # NOTE : you see 'None' here since backward() hasn't been executed yet.

               None

           Bias gradient :

              None

 

Now define a input to the network.

    x = torch.tensor([[1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                tensor([[1., 1.]])

 

Now define the equation to calculate the output value (this is called 'Forward' procedure). It is up to you how you defined this procedure. In this example, I defined as follows.

    o = torch.nn.Sigmoid().forward(net.forward(x))

    print('Output :\n',o)

    ==> Output :

                tensor([[0.6254]], grad_fn=<SigmoidBackward>)

     

Now define the output value that you desire to get for the input values that you provided in previous step.

    t = torch.tensor([[1.0]])

    print('Target :\n',t)

    ==> Target :

             tensor([[1.]])

     

Then define the error function (loss fuction) between the desired output and the calculated output. It is up to you on how to define the loss function, but the simplest way is just to take difference between the desired output and the calculated output as shown below. For simplicity, I took the simple difference between the desired output and calculated output as a loss function, but you can use vaious different algorithms for the loss function definition as listed here.

    loss = t-o

    print('Loss :\n',loss)

    == > Loss :

             tensor([[0.3746]], grad_fn=<SubBackward0>)

     

Now based on this, you can calculate the gradient for each of the network parameters (i.e, the gradient for each weights and bias). To do this, just call backward() function as shown below.

    loss.backward()

     

Once the backward() function is executed, you can confirm that the gradient values are stored as shown below.

    print('Weight gradient \n',net.weight.grad)

    print('Bias gradient :\n',net.bias.grad)

    ==> Weight gradient

                tensor([[-0.2343, -0.2343]])

           Bias gradient :

                tensor([-0.2343])

 

One thing to notice here is that backward() function just calculate the gradient values, it does not change the weight and bias values. Try printing out the weight and bias and you can see those values remain unchanged as shown below.

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==>  Weight of network :

                   Parameter containing:

                          tensor([[0.1333, 0.6570]], requires_grad=True)

           Bias of network :

                   Parameter containing:

                          tensor([-0.2780], requires_grad=True)

 

 

 

Back Propagation

 

The procedures to be implemented in this section can be summarized as follows. Step 1~7 is exactly same as the procedure we went through in previous section. Step 8 is the main step in this section.

 

Step 1

Define a Network

Step 2

Create a sample Input Data

Step 3

Define a procedure to caclulate the Output (this is called 'Foward' procedure)

Step 4

Define the desired output for the input data

Step 5

Calculate the Output data (Estimated Output) using the input and Forward procedure(Step 3)

Step 6

 Calculate the Error from the Estimated Output and Desired Output. This Error is called 'Loss'

Step 7

 Caculate the gradient

Step 8

 Update Weight and Bias based on the graident values (Backpropagate the nework parameters)

 

 

    import torch

     

    net = torch.nn.Linear(2,1);

    print('network structure : torch.nn.Linear(2,1) :\n',net)

    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> network structure : torch.nn.Linear(2,1) :

                  Linear(in_features=2, out_features=1, bias=True)

           Weight of network :

                  Parameter containing:

                         tensor([[ 0.4633, -0.4838]], requires_grad=True)

           Bias of network :

                  Parameter containing:

                         tensor([0.2706], requires_grad=True)

     

     

    print('Weight gradient \n',net.weight.grad)

    print('Bias gradient :\n',net.bias.grad)

    ==> Weight gradient

                 None

           Bias gradient :

                 None

     

     

    x = torch.tensor([[1.0,1.0]])

    print("input = x :\n ",x)

    ==> input = x :

                tensor([[1., 1.]])

     

     

    o = torch.nn.Sigmoid().forward(net.forward(x))

    print('Output :\n',o)

    ==> Output :

               tensor([[0.5622]], grad_fn=<SigmoidBackward>)

     

     

    t = torch.tensor([[1.0]])

    print('Target :\n',t)

    ==> Target :

             tensor([[1.]])

     

     

    loss = t - o

    print('Loss :\n',loss)

    ==> Loss :

             tensor([[0.4378]], grad_fn=<SubBackward0>)

     

     

    loss.backward()

     

     

    print('Weight gradient \n',net.weight.grad)

    print('Bias gradient :\n',net.bias.grad)

    ==> Weight gradient

                tensor([[-0.2461, -0.2461]])

           Bias gradient :

                tensor([-0.2461])

     

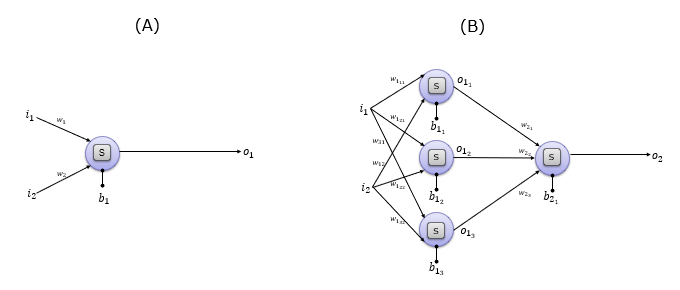
    print('Weight of network :\n',net.weight)

    print('Bias of network :\n',net.bias)

    ==> Weight of network :

                  Parameter containing:

                         tensor([[ 0.4633, -0.4838]], requires_grad=True)

           Bias of network :

                  Parameter containing:

                         tensor([0.2706], requires_grad=True)

     

Now update the nework parameters (weights and bias) using the gradient values calculated above. There are many different algorithms on how to update the weights and bias as described here. I just picked one of the algorithms as shown below.

    optimizer = torch.optim.SGD(net.parameters(), lr=0.05)

    optimizer.step()

 

Now you can confirm that the wieght and bias values are updated as shown below.

    print('New Weight of network :\n',net.weight)

    print('New Bias of network :\n',net.bias)

    ==> New Weight of network :

                 Parameter containing:

                        tensor([[ 0.4756, -0.4715]], requires_grad=True)

           New Bias of network :

                 Parameter containing:

                        tensor([0.2829], requires_grad=True)

     

     

 

Next Step

 

Now I assume that you got familiar to some degree with how to represent the single layered linear network. What about some other cases as shown below. How about followings ? Do you think you can implement these network with Linear() only ?

(A) is still single cell network. You may think you can implement this with Linear() only. But if you take a little bit more carefull look, you would notice on a different thing. This neuron has a small rectangle within the cell marked as 'S'. This little rectangle is called Activation function. 'S' indificates a specific type of Activation called 'Sigmoid'. You cannot represent this network even though it is single cell because Linear() function because Linear() does not have any built in Activation function.

(B) is made up of four neuron (every neuron has activation function in it) and it is made up of two layers. The first layer is made up of 3 neurons and the second layer is made up of 1 neuron. You cannot implement this kind of multi-layer network with Single Linear() function.

In these case, you need to combine multiple functions like multiple Linear() function or Linear()+Activation function etc. This is where you need to use another type of network construction method like nn.Sequential or nn.Module.