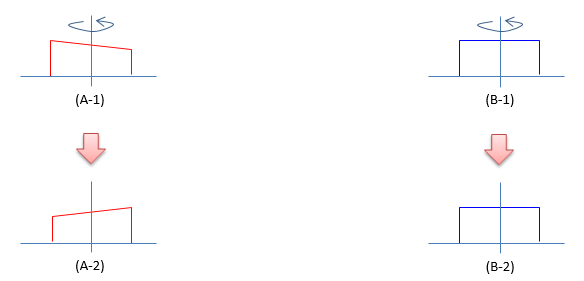|
RF |
||
|
RF Front End - Rx Chain Tutorial
When I am trying to learn anything in technology (pure science or engineering), usually I assume a blackbox and define inputs(first step) and output(last step), and then write down all the intermediate steps as much as I can think of. I found this has been pretty useful approach for me. Even though this may sound simple, but it would not be that easy when you really tries. Gathering information (knowledge) about those intermediate steps just by reading textbooks and industry standards would take huge amount of time and efforts. One of the best way to do this is to have an experts in the area and get some professional tutoring. Yes... I know this is not easy either. First, finding the expert around yourself would be difficult and finding the experts who has williness and capability to explain things in a way that beginners to understand would be even more difficult. Fortunately I came to know an expert who turned out to be the best fit for me and this tutorial is from the chat for about an hour in front of a whiteboard. His name is Hong Kirby.
Overall Procedure (Scope of the tutorial)
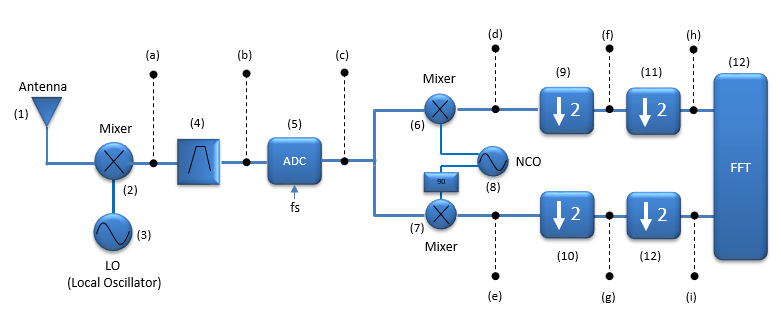
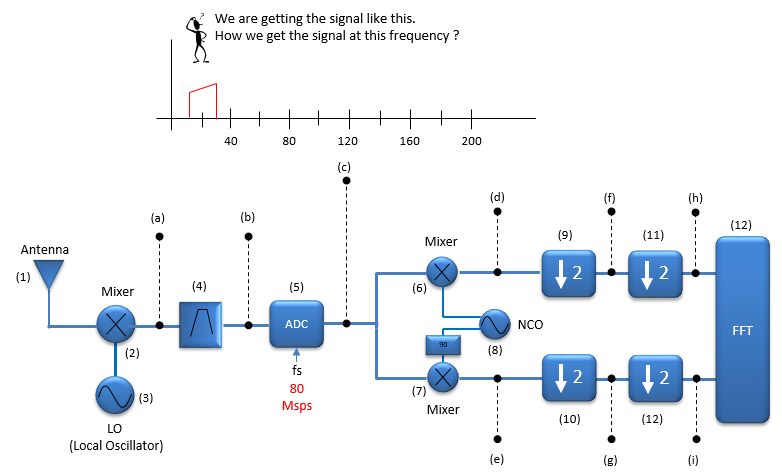
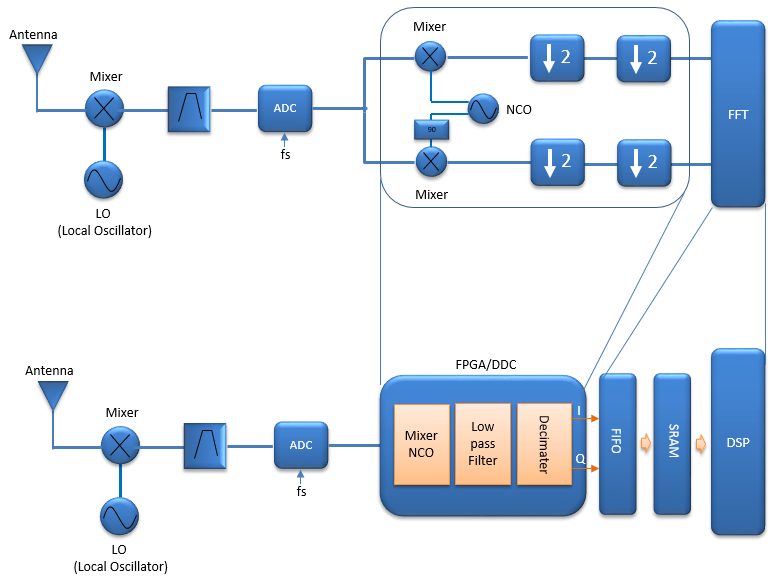
The scope of this tutorial is illustrated as below. My goal is to go through this block from the beginning (Antenna) through the end(FFT block) in this case. This is just an example of an reciever chain that I am interested in. The details would vary depending on the specific application of the reciever chain. In this tutorial, my focus would be mostly around (a)~(i) and (4)~(12). I would not talk much of (1),(2),(3) and (12) in this page.
Starting Point
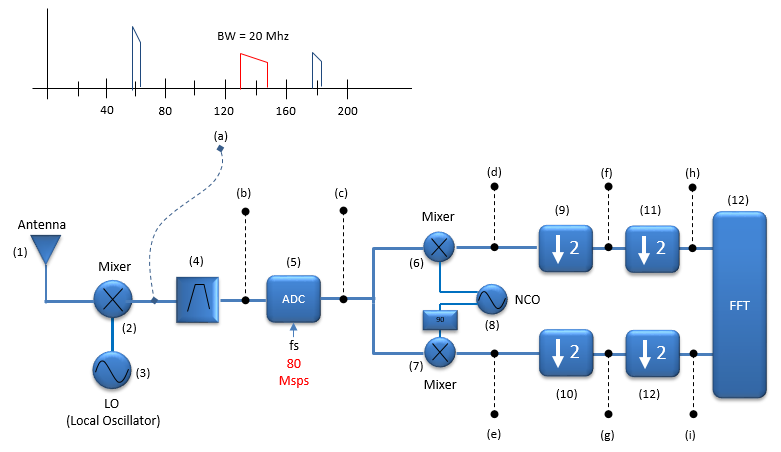
Even though the block diagram starts with Antenna, my focus in this page is more of processing an IF analog signal to baseband digital signal which is about to get into DSP process. In this block, we assume that the LO(3) and Mixer(2) downconverts the signal always to the frequency of 140 Mhz as marked in red in the plot(a) shown below.
Stupid Question ?
This may not sound so technical .. but I have this question for quite a long. When I first got into this field (wireless / celluar communication) without much theorectical background, I just started with playing with various equipments like signal generator, spectrum analyzer, network analyzer etc. If you take a measurement of frequency response for any real life signal or real life RF devices you would see pretty flat and symmetric (symmetric at least in passband section) as illustrated as shown in (B). But when I see the textbook or articles about DSP(digital signal processing), I noticed the frequency domain wave form is represented as an asymmetric form as shown in (A). I've been wondering for a while, why they draw it like this.
The simple answer is to represent the case of spectral inverse (spectral flipping). In the process of digital processing, there are cases where the spectrum (frequency domain waveform) flips around. If we represent the waveform in symmetric, it is impossible to recognize whether it is 'inversed spectrum(flipped spectrum)' or the original spectrum as in (B) shown below. If we represent the waveform in asymmetric form, it is easy to make the difference between the orignal form and inversed form as in (A) shown below.
Now you may ask 'why and when this kind of spectral inversion happens ?'. This is not a scope of this tutorial, but it is good question. Refer to Ref [1] or Ref[2] if you are seriously interested on it.
Filtering IF signal
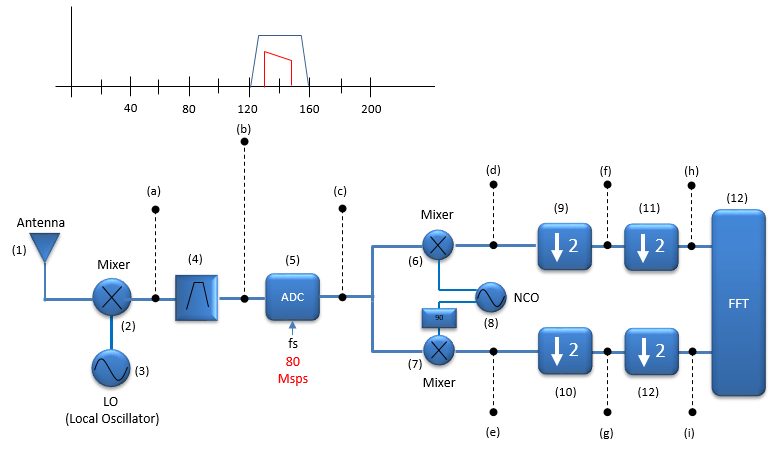
The first step after downconverting the RF to IF signal is to bandpass filter the signal as shown below. This process itself would be simple. Just passing the signal into a passive device (IF Bandpass Filter). The main purpose of this process is to deliver the clean signal (i.e, no noise outside of the signal passband area) to ADC.
Converting Analog to Digital (Sampling)
This step is the critical step in most of the modern RF front communication for digital communication system. It is to sample the analog IF signal into a sequence of digital data. Assuming that the signal is sampled at the rate of 80 Msps, the signal frequency after the digitization would be shown as follows. Now you may notice that the signal frequency shown below doesn seem to be correct (at least, intuitive).
The first question that might come up to your mind would be 'why sampling at 80 Msps, not 170 (the highest frequency of the IF signal coming into ADC) ?'. Isn't this the violation of Nyquist sampling criteria ? You would see that it is not the violation of Nyquist sampling criteria in this case(See Sampling Theory page). Actually 80 Mhz is oversampling of the signal.
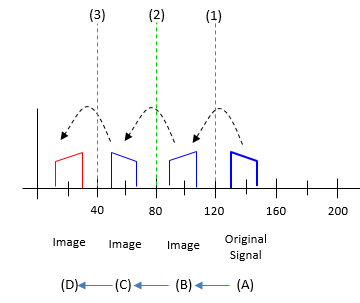
Next question popping up in your mind would be 'How the sampled signal frequency get so low ?'. One of the most important law in Digital Signal Processing(DSP) would be 'If you digitize an analog signal into digital data, always multiple number of image signal are generated (actually infinite number of image signal are generated if you observe the signal from -Infinity to +Infinity). In this case, the original signal is (A) shown below. When this is digitized at 80 Msps, the image is generated as (B) -> (C) -> (A). In most case, this kind of image is regarded as something unwanted (i.e, something to be removed), but in this case we actively use one of these image. We will use an image marked in red as the signal as the result of the sampling (ADC). In short, by this mechanism we can get the signal at the center frequency of fs/4 (4th of the sampling frequency). At this specific example, we used the sampling frequency of 80 Mhz. So the digitized data frequency we get is 20 Mhz (=80/4) as shown below.
At this point, you may have another question. What is the selection criterial for the ADC sampling frequency ? There can be a couple of factors determining this as follows.
Pusing the frequency down to Baseband
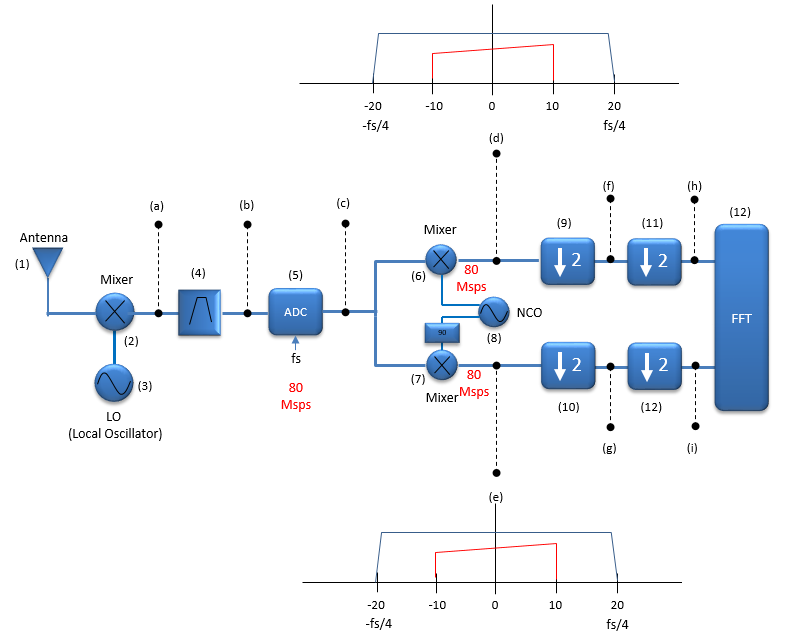
As shown above, from ADC we got the digitized signal very close to the baseband but the center frequency is still away from 0 frequency. How do we push the center frequency of the signal down to 0 ? The logic is same as in Analog signal processing. Using the mixer and local oscillator, we can push it down to 0 frequency (baseband) as shown below. The only difference from analog frequency conversion is that we are using a digital local oscillator (NCO : Numerically Controlled Oscillator) instead of the analog oscillator. After this mixing process, the signal will be positioned at 0 frequency as shown in red below.
With this step, we get the data that can be forwarded to the DSP blocks. Theoretically this can be all we need in terms of digitization. However, we will do some additional process to reduce the number of data without losing the nature of the signal as will be explained in following section.
Reducing the number of samples
As mentioned above, theoretically the previous step (i.e, downconvert the digital signal to baseband). However, we are trying to do some additional steps to reduce the number of data without losing the nature of the signal. Why do we need to do this ? Reduced number of sample mean that DSP block can process the data with less number of operation. It means it can reduce the requirement of DSP chips in terms of processing power which would mean lowering the cost and also reduce power consumtion as well.
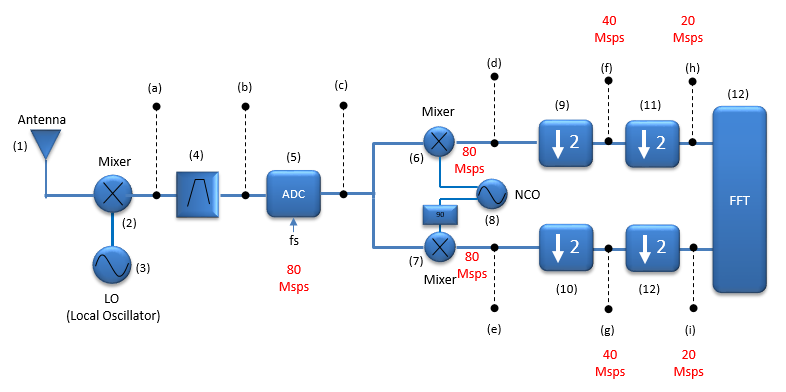
First step is (9) and (10) which downs-samples the signal by 2. The reason behind this is... when a signal is separated into I and Q, we can downsample the data by two without losing the nature of the original data. With this specific example, the signal bandwidth is 20 Mhz and after this step we get I and Q with 40 Msps as indicated at (f) and (g). If this is not the I/Q data, this would be the best we can do which 40 Msps is the Nyquist limit of 20 Mhz BW signal. But since this is I/Q data, we can do one more downsample-by-2 for I and Q as indicated by step (11) and (12). In this specific example, we get I data with 20 Msps and Q data with 20 Msps as indicated in (h) and (i).
More questions ?
We have gone through overal signal flow along a RF Rx chain and I think (hope) you would get the general idea on how it works. Now take a look at the original diagram again and see how much you can explain about this on your own words.
While going through each components of the path, you may get a lot of other questions boggling in your mind. Followings are the list of questions that popped up in my mind and the list gets longer as I think more in detail.
How to determine the IF frequency (i.e, the frequency at point (a)) ?
There are several factors determining on this and the answer may vary a little bit of the overall design and application, but followings would be major factors.
How to determine the bit resolution of ADC ?
Theoretically ADC Bit Resolution determines the accuracy of the digitized sample, i.e, the degree of quantization error (See ADC page for the basic principle of ADC). As the bit resolution gets larger, the quantization error gets smaller. As quantization gets smaller, you would get better SNR for the signal coming out of the ADC. Roughly if you increase the bit resolution of ADC by 1, you would get around 6 dB gain in SNR (See here for further details). Simply put, if you use an ADC with higher bit resolution you would get better signal. But downside would be that you would need higher processing power and memory requirement.
In most of RF application, the signal frequency(channel frequency) coming into the antenna(1) varies, but eventually the center frequency of the signal should go down to 0(baseband) at the point (d). How do we get the varying signal frequency down to a constant frequency(i.e, 0 frequency) ? By changing LO(3) frequency ? or by changing NCO(8) frequency ?
The answer may vary depending how you design/implement the overall reciver path. But the most common answer would be 'By chaning LO(3) frequency'. It means we usually design the RF reciever path in such a way that IF frequency is always same regardless of the signal frequency coming into Antenna. Why ? If the IF frequecy varies, we need to use a lot of different IF filters(4) with different center frequency which is not practical in many ways.
How downsampling (9,10,11,12) works ? Is it just taking a few data away from the original data in a certain interval ?
Where is FIFO(First In First Out) and DSP involved in this process ?
Reference :
[1] Handling Spectral Inversion in Baseband Processing [2] Spectral Flipping Around Signal Center Frequency [3] A Quadrature Signals Tutorial: Complex, But Not Complicated [5] SNR to Resolution converter [6] Designing a 256-Channel Digital Downconverter
|
||