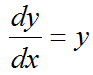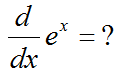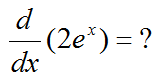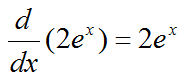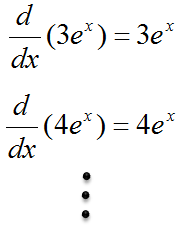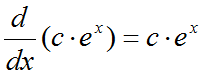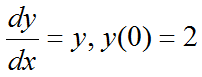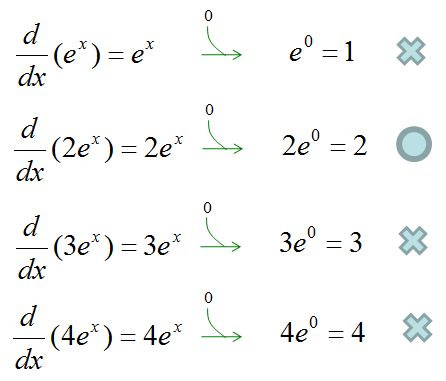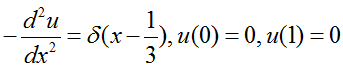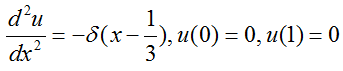|
Engineering Math - Differential Equation |
||
|
Intuitive Solution
This page is to give you some intuitive understanding of meaning of several patterns of differential equations, not too much about the solution itself. In real life, you wouldn't find many of differential equation which can be solved intuitively as described in this page. But the way I describe in this page would give you more familiarity to various differential equations and I hope you can be less "scared" about differential equation. However, I expect you to have some previous exposures to the concept of basic calculus like the concent of derivatives.
First pattern of differential equation I want to look into is as follows.
Now just try to vervalize the meaning of this equation based on what you learned in basic calculus course. I can describe it as follows. i) There is a function called y(x) ii) The first derivative of y(x) equals to itself (y(x)).
The only thing you have to do now is to make some GUESS on what kind of function has the characteristics as mentioned above. Actually it would not be easy to make a guess if you do not have any knowledge about calculus. But if you just look into well known tables like this, you may find a function that meets this requirement. It is the exponential function.
Then what is the first derivative of y ?
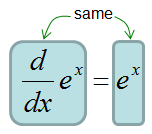
The answer is as follows. You see the function e^(x) satisfy the equation and property saying "The first derivative of y(x) equals to itself (y(x))". If you can find another function meeting the requirement, that can be the solution for this differential equation.. or if you can even create your own function whatever it is, that can be the solution too.
Is this the only function that satisfy the equation ?
Now let take another function and plug into the equation. I chose the function y(x) = 2 e^(x) in this case
What is the answer ? It is as follows. From this, you see 2 e^(x) also meets the criteria of "The first derivative of y(x) equals to itself (y(x))". So 2 e^(x) can be a solution for the differential equation.
Now let's try to find some other functions. As you see in the following example, you would find the infinite number of functions that can be the solution to the differential equation given in this example.
Based on all the functions that we found above, you can come out with a general form of equation as follows.
According to the equation above, you can say a generic function shown below meets the differential equation. This is called a general solution for the equation.
In previous example, you could find a solution to a differential equation based on the intuitive interpretation of the equation itself and simple derivative table. One problem was we had too many solution to the equation. It is not because our method is wrong, but because we have not enough information to pick any one specific function as the solution. Now let's look at another differential equation as shown below. The first part is exactly same as in the previous example. The only difference is that we have one additional information (This kind of additional information is a boundary condition or boundary value. or in this example case, it is called 'initial value' or 'initial condition' because it gives only a single condition at the starting point)
As we did in previous example, let's verbalize this equation. (let's describe the equation in plain language). It is as described below. i) There is a function called y(x) ii) The first derivative of y(x) equals to itself (y(x)). iii) There is one condition saying "y(0) should be 2". It means the value of the function y(x) at the point x = 0 is 2. The way you can find solution for this kind is equation is a) Find all the possible solution to a give differential equation b) Plug the additional information into the all the candidate solution, and pick a specific function that meets the boundary condition.
We already did step a) in previous example.. so I would not redo this step. Now let's do step b). If you plug the initial condition (y(0) == 2) into the all the candidate function (general solution) that we got from step a), only one function meets the give initial condition as shown below. So y(x) = 2 e^x is the solution for the differential equation in this example.
This example would not be as intuitive as previous example and you would not found the solution from the tables in a calculus book. But I put this as an example since it can greatly help you with the concept of 'Green Function'.
Let's suppose we have a second order differential equation as shown below. At first part we have a differential equation and in second, the third we have boundary conditions.
Just a little modification, we can rewrite the equation as follows. You don't have to do this, but I did this form matches better with the graphical representation that we will go through.
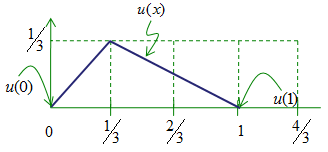
How can we find the solution to this equation ? Unfortunately it is not that straightforward and I would not explain it in this page now. In stead, let's just suppose that we are given a function and check if the given function meets the given differential equation.
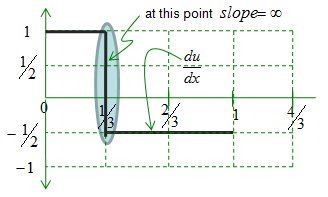
Now let's take the first derivative of this function. It is easy.. it is like figuring out the slope of a graph that you learned in high school physics and math. If you plot the first derivative (u'(x)) in a graph, you would get a plot as shown below. (Note that it looks like a step function).
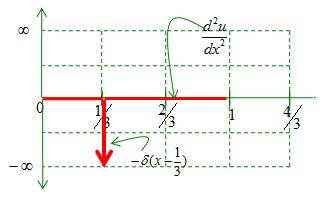
Now let take another derivative of the above graph. Since this is derivative of the first derivative, it became the second derivative of the original function. The graph looks as follows and now you can realize that the second derivative of the given function (u''(x)) matches the given differential equation.
|
||