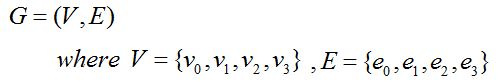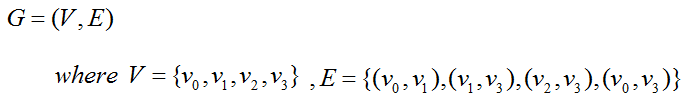Engineering Math - Graph Theory

Notation (Mathematical Representation)

If you read the What is Graph ? page, you might have thougt 'Ohm.. it is interesting concept. it doesn't look as hard and boring as other mathematical topics'. and if you went through 'Terminology' page, 'Pretty many technical words.. but I think I can digest it to some degree', but Graph Theory is also a part (branch) of mathematics. The area is also using a lot of mathematical symbols and mathematical representations and you have to get familiar with those notations (representations) if you want to do serious study on this subject.

There are several different ways of representing a graph and you will see various different forms from different text books or papers etc. Some of the firm may look a little bit easier or more familiar and some of them may look pretty intimidating (daunting/scary) to you. Don't get scared away from this topic just because of those mathematical symbols, just try to pick up any form which would look the most familiar to you and search a lot of materials (books, web pages etc) that are using the same/similar form until you get fully familiar with the concept and then you can extend it to other forms of representation piece by piece.

Followings are several different forms of representation and this list will keep being extended as I come across more forms and find time for update.

Example 1 >

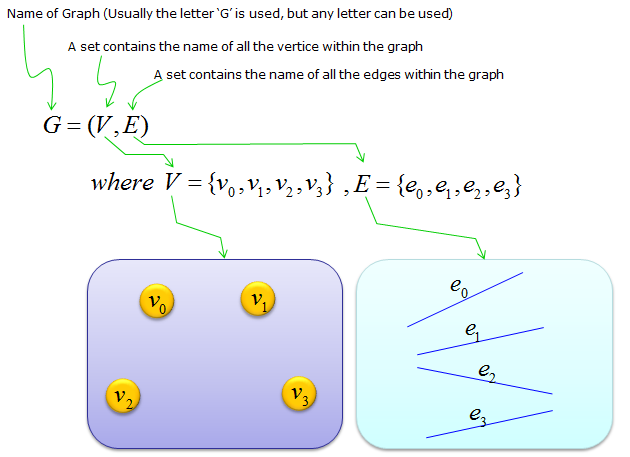
This would be the most simplest form of representation.

The meaning of this is as follows. It simply says "We have a graph called 'G' and the graph is made up of the vertice V and the edge E". It does not say anything about how many vertices are in the graph and how many edges are in the graph. But this presentation is still be widely used in pure theoretic text and it implies 'the theory (theorem, rules etc) is applied to any type of graph'.

Example 2 >

This has a little bit more information of the graph comparing to the first example.

The meaning of this representation is as follows.

Does this have enough information with which you can draw a specific graph ?

Still No. It does not have the information on which edge is connecting which vertice. In order to draw a specific graph, you would need adjacent matrix and incidence matrix or you should use another form of representation.

Example 3 >

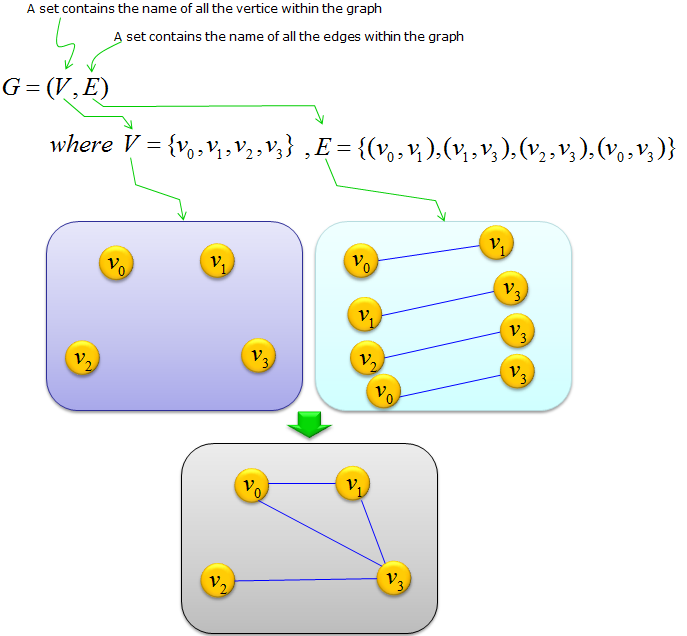
Following is a form that contains enough information that you can at least draw a graph. (It is still missing some information about the direction of the edges, but at least you can draw a graph which is not 'directed' (non-directed graph). This type of definition goes as follows.

Detailed meaning of this definitiona can be illustrated as follows. As you see, you can come out with a complete graph (diagram) from the definition itself.